Vectors and conic sections - Part 3
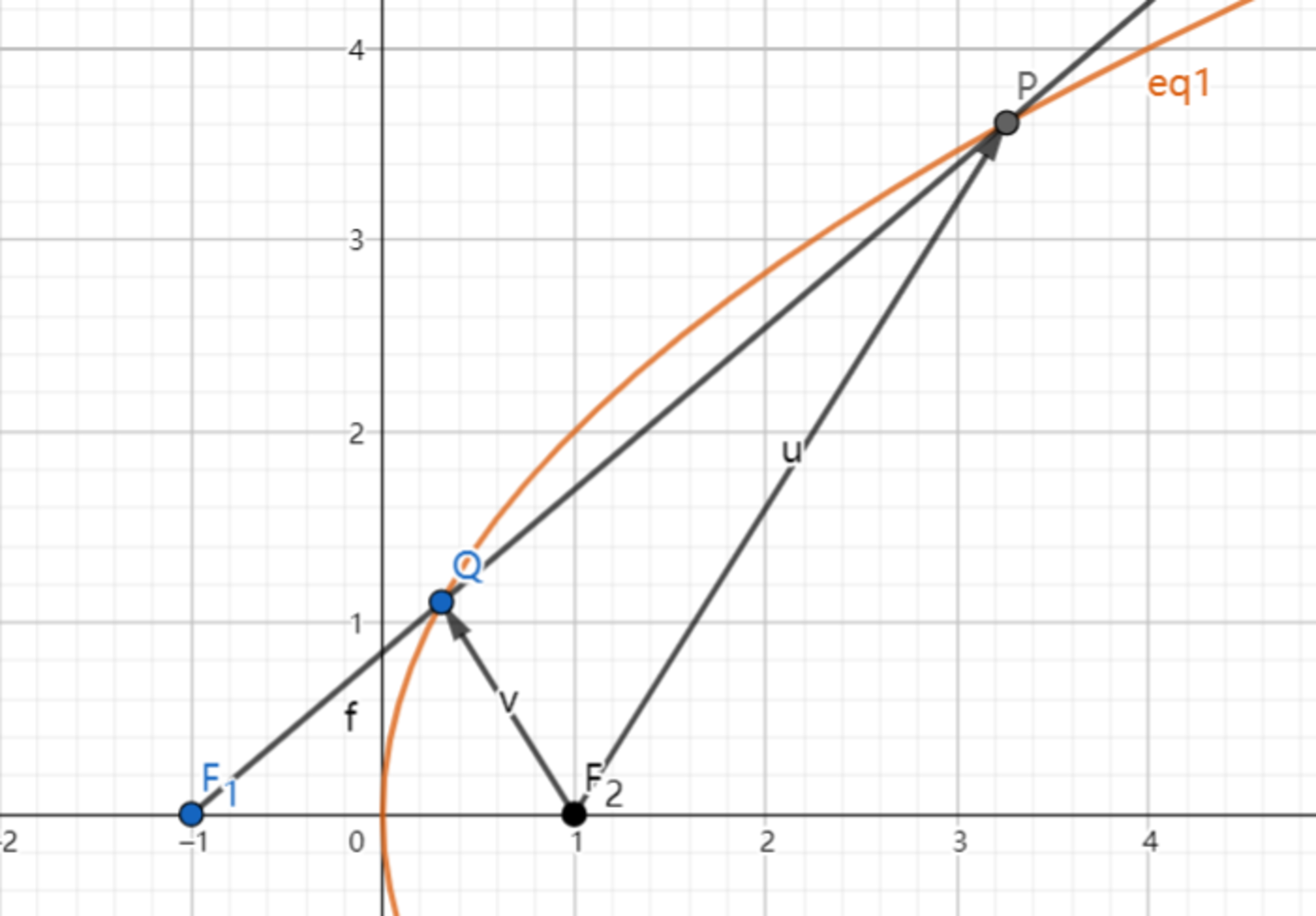
As shown above, F 1 ( − 1 , 0 ) , F 2 ( 1 , 0 ) . line l passes through F 1 and intersects with the parabola y 2 = 4 x at point P , Q . Given that F 1 P = λ F 1 Q , where λ ∈ [ 2 , 3 ] , find the range of F 2 P ⋅ F 2 Q .
If the range can be expressed as [ l , r ] , submit ⌊ 1 0 0 0 0 ( r − l ) ⌋ .
The answer is 8333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the equation of F 1 P be y = m ( x + 1 ) , the position coordinates of points P , Q be ( h 2 , 2 h ) , ( k 2 , 2 k ) respectively. Then the given equation implies
λ 2 ( ( k 2 + 1 ) 2 + 4 k 2 ) = ( h 2 + 1 ) 2 + 4 h 2
Solving the equations of the parabola and the straight line we get
m 2 ( x + 1 ) 2 − 4 x = 0 , whose roots are h 2 , k 2 . So h k = 1 ⟹ k = h 1 .
Therefore λ 2 ( ( h 2 1 + 1 ) 2 + h 2 4 ) = ( h 2 + 1 ) 2 + 4 h 2 ⟹ h 2 = λ .
Now, F 2 P . F 2 Q = 6 − ( h 2 + h 2 1 )
So, r = 6 − 2 . 5 = 3 . 5 , l = 6 − 3 1 0 = 3 8 = 2 . 6 6 6 6 6 6 . . . , and r − l ≈ 0 . 8 3 3 3 3 3 3 ⟹ ⌊ 1 0 0 0 0 ( r − l ) ⌋ = 8 3 3 3
Let the coordinates of P ( x p , y p ) and Q ( x q , y q ) . Since F 1 is on the directrix and F 2 is the focus of the parabola, this means that x p + 1 = ∣ F 2 P ∣ = u and x q + 1 = ∣ F 2 Q ∣ = v as shown in the figure.
Since ∣ F 1 Q ∣ ∣ F 1 P ∣ = x q + 1 x p + 1 = ∣ F 2 Q ∣ ∣ F 2 P ∣ = v u = λ ⟹ u = λ v . Also ∣ F 1 P ∣ = ( 1 + x p ) 2 + y p 2 = u 2 + 4 x p = u 2 + 4 u − 4 ; similarly, ∣ F 1 Q ∣ = v 2 + 4 v − 4 . As ∣ F 1 P ∣ = λ ∣ F 1 Q ∣ , we have:
u 2 + 4 u − 4 u 2 + 4 u − 4 λ 2 v 2 + 4 λ v − 4 4 λ ( λ − 1 ) v ⟹ v = λ v 2 + 4 v − 4 = λ 2 ( v 2 + 4 v − 4 ) = λ 2 v 2 + 4 λ 2 v − 4 λ 2 = 4 ( λ 2 − 1 ) = λ λ + 1 Since u = λ v
Now ∣ F 2 P ∣ ⋅ ∣ F 1 Q ∣ = u v = λ v 2 = λ ( λ + 1 ) 2 ⟹ { λ = 2 λ = 3 ⟹ u v = 2 9 ⟹ u v = 3 1 6 ⟹ ⌊ 1 0 0 0 0 ( r − l ) ⌋ = 8 3 3 3 .