Vectors and conic sections - Part 4
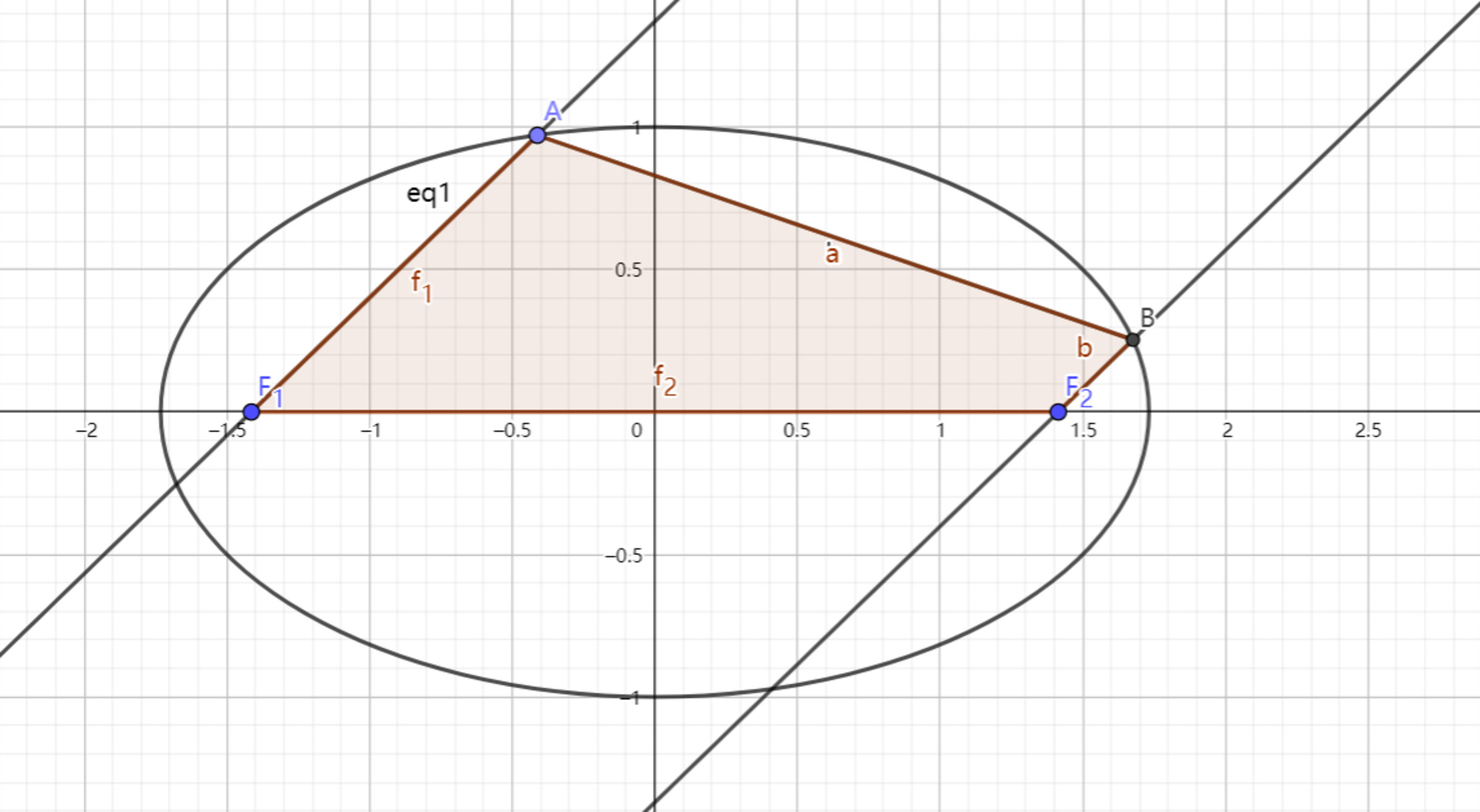 As shown above, the ellipse has the equation:
3
x
2
+
y
2
=
1
, whose left and right focus points are
F
1
and
F
2
respectively.
A
and
B
are two points on the ellipse and they are both
above
the
x
-axis.
As shown above, the ellipse has the equation:
3
x
2
+
y
2
=
1
, whose left and right focus points are
F
1
and
F
2
respectively.
A
and
B
are two points on the ellipse and they are both
above
the
x
-axis.
Given that F 1 A = 5 F 2 B , find the area of quadrilateral A B F 2 F 1 .
If the area is A , submit ⌊ 1 0 0 0 0 A ⌋ .
Note: The picture above just shows a particular case where F 1 A ∥ F 2 B .
The answer is 16970.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The given condition F 1 A = 5 F 2 B implies that the lines of action of those two vectors are always parallel. Let the equation of F 2 B be y = m ( x − 2 ) and that of F 1 A be y = m ( x + 2 ) (the position coordinates of F 1 are ( − 2 , 0 ) and of F 2 are ( 2 , 0 ) ).
Then the area of the trapezium A B F 2 F 1 is 2 1 ( ∣ A F 1 ∣ + ∣ B F 2 ∣ ) p , where p = 1 + m 2 2 2 m is the perpendicular distance of B F 2 from F 1 .
That is, the area is 1 + m 2 6 2 m ∣ B F 2 ∣ .
Now, solving the equations of the ellipse and A F 1 for positive x -value we get the x coordinate of A as x A = 1 + 3 m 2 3 ( 1 + m 2 ) − 3 2 m 2
Similarly, we get the x coordinate of B as x B = 1 + 3 m 2 3 ( 1 + m 2 ) + 3 2 m 2 .
So, ∣ A F 1 ∣ 2 = ( 1 + 3 m 2 ) 2 1 + m 2 ( 3 ( 1 + m 2 ) + 2 ) 2 ,
∣ B F 2 ∣ 2 = ( 1 + 3 m 2 ) 2 1 + m 2 ( 3 ( 1 + m 2 ) − 2 ) 2 . The given condition ∣ A F 1 ∣ = 5 ∣ B F 2 ∣ yields m 2 = 2 1 ⟹ ∣ B F 2 ∣ = 5 3 .
Therefore the required area is 2 3 6 2 × 2 1 × 5 3 = 1 . 2 × 2 ≈ 1 . 6 9 7 0 5 6 .
Hence the required answer is 1 6 9 7 0 .
Answer to the problem "Vectors and conic sections - Part 2"
Let the position coordinates of Q and R be ( k , m − 2 k ) and ( h , m − 2 h ) respectively, and the required ratio be α . Then h = α k .
Solving the equations of the hyperbola and the straight line we get x 2 − 4 m x + m 2 + 3 = 0 , whose roots are h , k .
Then the given equation yields 2 m + 3 ( m 2 − 1 ) = 2 α m − α 3 ( m 2 − 1 ) ⟹ α 2 − 1 4 α + 1 ≤ 0 ⟹ α ≤ 7 + 4 3 .
Since the minimum value of α is 1 when the line touches the hyperbola, the range of α is [ 1 , 7 + 4 3 ] .
So r = 7 + 4 3 , l = 1 ⟹ r − l = 6 + 4 3 , and ⌊ 1 0 0 0 ( r − l ) ⌋ = 1 2 9 2 8 .
Draw diagonals F 2 A and F 1 B , and extend A B and F 1 F 2 to meet at C . Let p = F 2 B and q = A B . Since F 1 A = 5 F 2 B , F 1 A = 5 p and F 1 A ∣ ∣ F 2 B .
By the properties of an ellipse with an equation 3 x 2 + y 2 = 1 , the distance between the foci is F 1 F 2 = 2 3 − 1 = 2 2 , and F 1 A + F 2 A = F 1 B + F 2 B = 2 3 . Therefore, F 2 A = 2 3 − 5 d and F 1 B = 2 3 − d .
Since F 1 A ∣ ∣ F 2 B , ∠ F 1 A F 2 = ∠ A F 2 B and ∠ F 1 B F 2 = ∠ A F 1 B as alternate interior angles.
By the law of cosines on △ F 1 A F 2 and △ A F 2 B , cos ∠ F 1 A F 2 = cos ∠ A F 2 B = 2 ( 5 p ) ( 2 3 − 5 p ) ( 5 p ) 2 + ( 2 3 − 5 p ) 2 − ( 2 2 ) 2 = 2 p ( 2 3 − 5 p ) p 2 + ( 2 3 − 5 p ) 2 − q 2 , which rearranges to:
q 2 = 1 6 p 2 − 1 6 3 p + 5 5 6 .
Similarly, by the law of cosines on △ F 1 B F 2 and △ A F 1 B , cos ∠ F 1 B F 2 = cos ∠ A F 1 B = 2 p ( 2 3 − p ) p 2 + ( 2 3 − p ) 2 − ( 2 2 ) 2 = 2 ( 5 p ) ( 2 3 − p ) ( 5 p ) 2 + ( 2 3 − p ) 2 − q 2 , which rearranges to:
q 2 = 1 6 p 2 + 1 6 3 p − 8 .
These two equations solve to p = 5 3 and q = 5 2 2 2 , which means F 1 A = 5 p = 3 and F 2 A = 2 3 − 5 p = 3 .
By the law of cosines on △ F 1 A F 2 , cos ∠ A F 1 F 2 = 2 ( 2 2 ) ( 3 ) ( 2 2 ) 2 + ( 3 ) 2 − ( 3 ) 2 = 3 6 , which means sin ∠ A F 1 F 2 = 1 − ( 3 6 ) 2 = 3 3 .
Since F 1 A ∣ ∣ F 2 B , △ A C F 1 ∼ △ B C F 2 , so F 2 B F 2 C = F 1 A F 1 C , or p F 2 C = 5 p F 2 C + 2 2 , which solves to F 2 C = 2 2 , so F 1 C = F 1 F 2 + F 2 C = 2 2 + 2 2 = 2 5 2 .
The area of △ A C F 1 is then A △ A C F 1 = 2 1 ⋅ F 1 A ⋅ F 1 C ⋅ sin ∠ A F 1 F 2 = 2 1 ⋅ 3 ⋅ 2 5 2 ⋅ 3 3 = 4 5 2 .
Since △ A C F 1 ∼ △ B C F 2 and ratio of their lengths is F 2 B F 1 A = p 5 p = 5 , the ratio of their areas is 5 2 = 2 5 , so the area of △ B C F 2 is A △ B C F 2 = 2 5 1 A △ A C F 1 .
That means the area of the quadrilateral A A B F 2 F 1 = A △ A C F 1 − A △ B C F 2 = A △ A C F 1 − 2 5 1 A △ A C F 1 = 2 5 2 4 A △ A C F 1 = 2 5 2 4 ⋅ 4 5 2 = 5 6 2 .
Therefore, ⌊ 1 0 0 0 0 A ⌋ = ⌊ 1 0 0 0 0 ⋅ 5 6 2 ⌋ = 1 6 9 7 0 .