Vectors are Awesome!!
A line makes angles α , β , γ , δ with the four diagonals of a cube, then find the value of cos 2 α + cos 2 β + cos 2 γ + cos 2 δ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
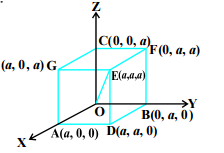 A cube is rectangular parallelepiped having equal length, breadth and height. Let OADBFEGC be the cube with each side of length
a
units. The four diagonals are OE, AF, BG and CD.
A cube is rectangular parallelepiped having equal length, breadth and height. Let OADBFEGC be the cube with each side of length
a
units. The four diagonals are OE, AF, BG and CD.
The direction cosines of the diagonal OE which is the like joining two points O and E are
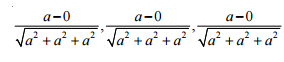
√ 3 1 , √ 3 1 , √ 3 1
Similarly, the direction cosines of AF, BG and CD are √ 3 − 1 , √ 3 1 , √ 3 1 ; √ 3 1 , √ 3 − 1 , √ 3 1 ; √ 3 1 , √ 3 1 , √ 3 − 1 respectively.
Let l , m , n be the direction cosines of the given line which makes makes angles α, β, γ, 𝛿 with OE, AF, BG, CD respectively.
Then, cos α = √ 3 1 ( l + m + n ); cos β = √ 3 1 ( − l + m + n )
cos γ = √ 3 1 ( l − m + n ); cos 𝛿 = √ 3 1 ( l + m − n )
Squaring and adding, we get
c o s 2 α + c o s 2 β + c o s 2 γ + \(cos^2 𝛿\) = 3 1 [ ( l + m + n ) 2 + ( − l + m + n ) 2 + ( l − m + n ) 2 + ( l + m − n ) 2 ]
= 3 1 [ 4 ( l 2 + m 2 + n 2 )
As l 2 + m 2 + n 2 = 1
3 1 [ 4 ( l 2 + m 2 + n 2 ) = 3 4
JEE Style
take the line as one of diagonal and angle between diagonal is cos inverse 1/3 so
1+1/9+1/9+1/9 = 4/3