Velocity of the Center of a Sliding Ellipse
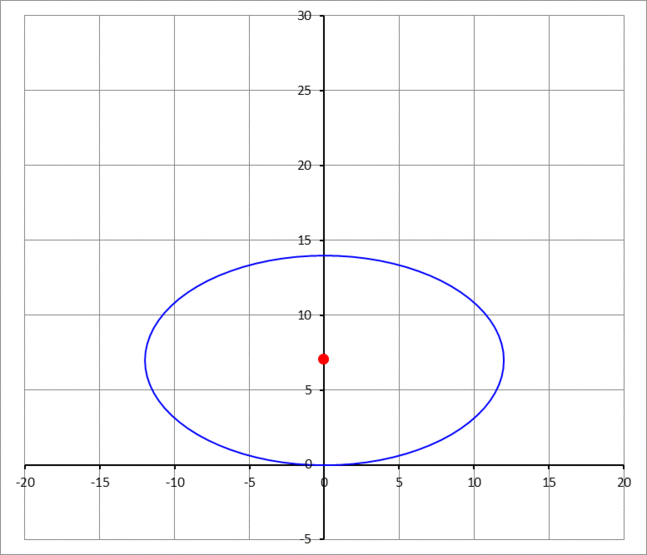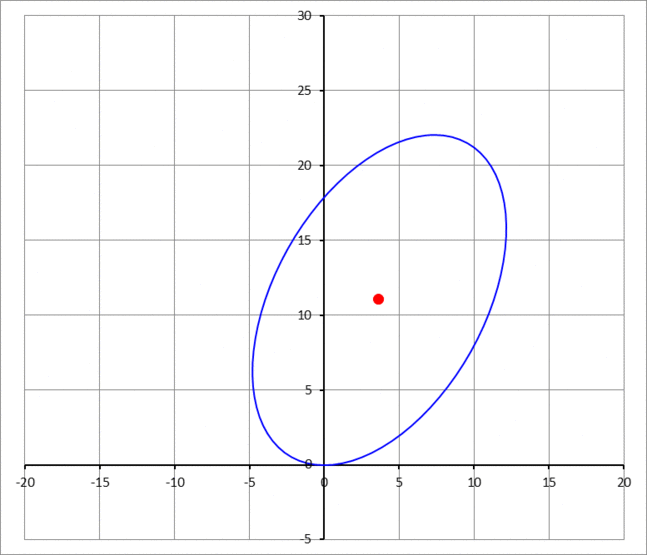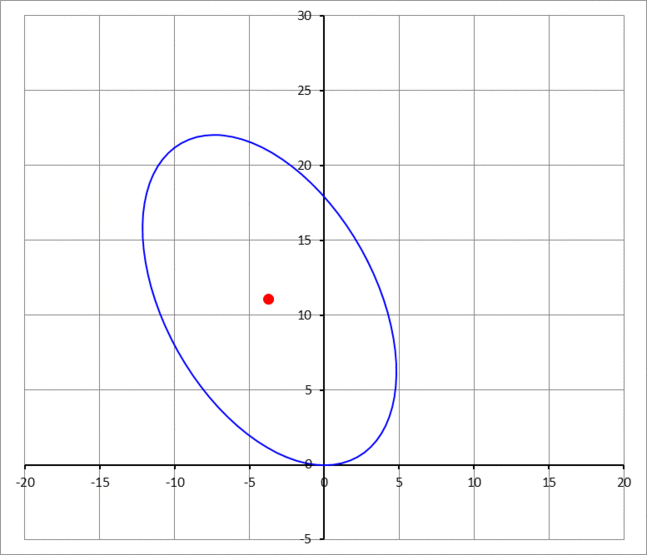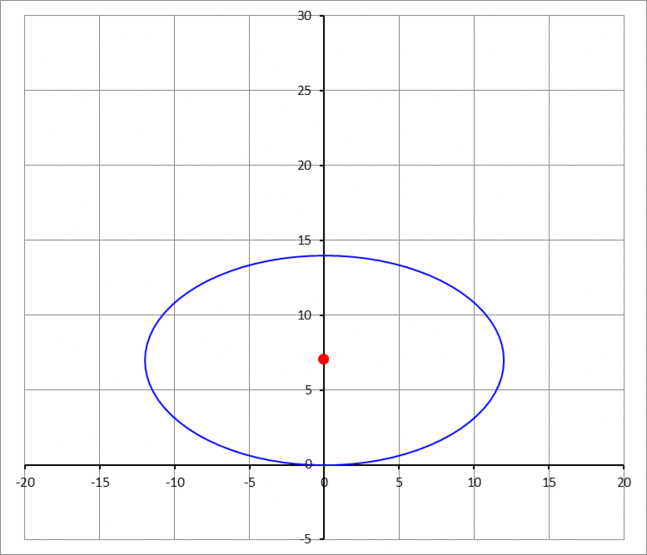
An ellipse with semi-major axis of 1 2 units and semi-minor axis of 7 units, is sliding in place at the origin of the Cartesian plane, as shown in the above GIF image. The angle of rotation θ of the ellipse is taken as zero when the major axis is parallel to the x -axis. If when θ = 4 π , the sliding point (the point of contact with the x -axis at the bottom of the ellipse) is moving with a speed of v 0 = 3 units/sec, what will be the velocity vector v C of the center of the ellipse?
If v C = ( v x , v y ) , then enter v x 2 + v y 2 as your answer.
The answer is 2.172175033.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thanks for solution. My approach was a little different as I exploit the parametric equation of the center of ellipse which I derived solving your other problem. Now when I've thoroughly checked my work, I noticed that I've made some foolish mistakes when I was differentiating. That's why I kept getting wrong results. After correction, I got result: 4 a 2 b 2 a 2 − b 2 2 ( a 4 + b 4 ) = 2 . 1 7 2 1 7 5 which matches with yours.
Excellent.
Probably the easiest way to solve this problem is to fix the ellipse and attach a reference frame (R, d) to a moving point on the perimeter of the fixed ellipse. Since the ellipse is moving counterclockwise, we want our point to move clockwise on the fixed ellipse. And this implies that this moving reference frame attached to the moving point will have an orientation of θ = − 4 π .
We can choose the x'-axis of the moving frame to point opposite to the time derivative of p , and the normal y'-axis is just a counterclockwise rotation of the x' axis.
Let s ( t ) be our eccentric angle (a function of time t ), then
p ( t ) = ( − a sin s , − b cos s )
the parameter s has ds/dt > 0. Now the velocity of point p is
p ′ ( t ) = d t d p ( t ) = ( − a cos s , b sin s ) d t d s
The rotation matrix of the reference frame attached to the point p has its rotation matrix as follows
R ( θ ) = [ cos θ sin θ − sin θ cos θ ]
The first column of the above matrix is the x'-axis, and the second column is the y'-axis.
Comparing the first column of the matrix R with the negative of the vector p ′ , we deduce that
tan θ = − a b tan s
Thus from the given value of θ = − 4 π , we can compute the eccentric angle s .
Also, by differentiating the above formula w.r.t time, we obtain,
sec 2 θ d t d θ = − a b sec 2 s d t d s
which determines the relation between d t d θ and d t d s . To determine d t d s we take the magnitude of d t d p and equate it with the given speed of the tangency point. We have
v = ∣ p ′ ( t ) ∣ = d t d s a 2 cos 2 s + b 2 sin 2 s
Now, the reference frames relation is
q = p + R q ′
where q is the coordinate vector of any point in the absolute frame, and q ′ is the the corresponding coordinate vector with respect to the moving reference frame whose rotation matrix is R .
Differentiating with respect to time,
d t d q = d t d p + d t d R q ′ + R d t d q ′
if q = 0 (a fixed vector) , then
0 = d t d p + d t d R q ′ + R d t d q ′
Hence,
d t d q ′ = − R T d t d p − R T d t d R q ′
And this completes the solution.