velocity Tension!!
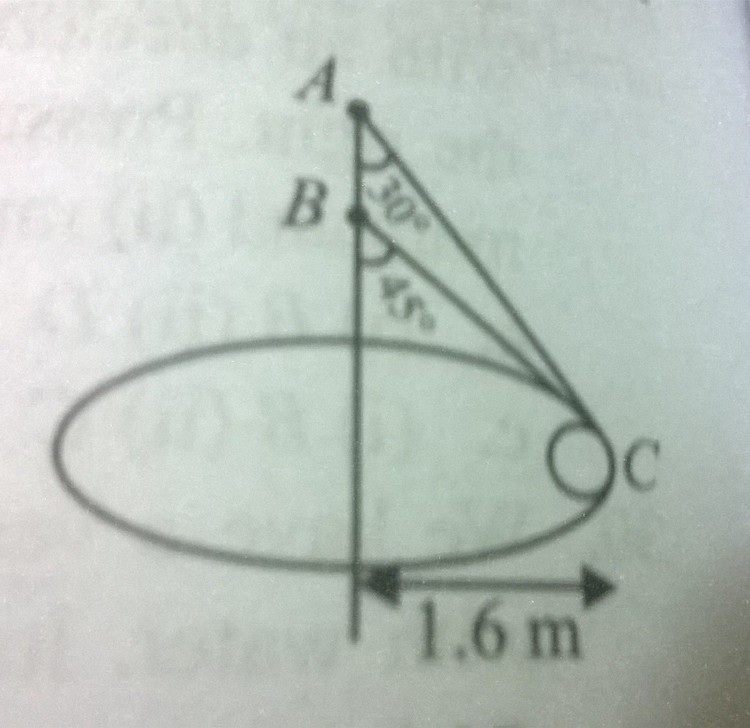 Two wires AC and BC are tied at C a small sphere of mass 5 kg ,which revolves at a constant speed V In the horizontal circle of radius 1.6 m . Find minimum value of V in S.I. UNITS .
Two wires AC and BC are tied at C a small sphere of mass 5 kg ,which revolves at a constant speed V In the horizontal circle of radius 1.6 m . Find minimum value of V in S.I. UNITS .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider the following free body diagram of the situation :
We find , applying Newton's second law in X- and Y-directions :
For X :
T 2 . s i n ( 3 0 ° ) + T 1 . s i n ( 4 5 ° ) = r m v 2 or 2 T 2 + 2 2 . T 1 = r m v 2 .
For Y :
T 2 . c o s ( 3 0 ° ) + T 1 . c o s ( 4 5 ° ) = m g or 2 3 . T 2 + 2 2 . T 1 = m g .
From the equilibrium in the Y-direction, we can find either :
2 2 . T 1 = ( m g − 2 3 . T 2 ) or
2 T 2 = ( 3 m g − 2 . 3 2 . T 1 ) ,
which we can plug into the equation for the X-direction to find either
2 2 . T 1 . ( 1 − 3 3 ) = m . ( r v 2 − 3 g ) or
T 2 . ( 2 3 − 2 1 ) = m . ( g − r v 2 ) .
Both these equations give a condition on v, because both tension forces need to be at least zero.
This means the right hand side determines the minimum value for v, since it should be at least zero, the terms between brackets determine a solvable equation for v, using g = 10 m/s and r = 1,60 m.
We find using the equation for T 1 that v should be a little more than 3 m/s.
Using the equation for T 2 we find that v should be at least 4 m/s.
=> 4 m/s .