Verifying Statements (Algebra)

If we square both sides of the original radical equation, we obtain:

$(1+b) + (1+c) + 2\sqrt{(1+b)(1+c)} = 4(1+a) \Rightarrow \frac{b + c - 2 + 2\sqrt{(1+b)(1+c)}}{2} = 2a$ (i)

Substituting (i) into the RHS of desired inequality above now yields:

$b+c \ge \frac{b + c - 2 + 2\sqrt{(1+b)(1+c)}}{2}$ ;

or $\frac{b+c}{2} + 1 \ge \sqrt{(1+b)(1+c)};$

or $b + c + 2 \ge 2\sqrt{(1+b)(1+c)};$

or $(b+c)^2 + 4(b+c) + 4 \ge 4(1+b)(1+c);$

or $b^2 + 2bc + c^2 + 4b + 4c + 4 \ge 4 + 4b + 4c + 4bc;$

or $b^2 - 2bc + c^2 \ge 0;$

or $\boxed{(b-c)^2 \ge 0}$

which is TRUE for all choices of $b,c \in \mathbb{R}.$

Here is my solution: $\sqrt{1+b}+\sqrt{1+c}=2\sqrt{1+a}$ $\Rightarrow (\sqrt{1+b}+\sqrt{1+c})^{2} = 4(1+a)$

Next, we use the inequality $(a+b)^2 \leq 2(a^2 + b^2)$ .

$\Rightarrow (\sqrt{1+b}+\sqrt{1+c})^{2} = 4(1+a) \leq 2(2+c+b)$ $\Leftrightarrow 2a \leq c+b$

Let $x = \sqrt{1 + a}$ , $y = \sqrt{1 + b}$ , and $z = \sqrt{1 + c}$ . Then $a = x^2 - 1$ , $b = y^2 - 1$ , and $c = z^2 - 1$ .

Substituting these values into the given equation $\sqrt{1 + b} + \sqrt{1 + c} = 2\sqrt{1 + a}$ gives $y + z = 2x$ , so $x = \frac{y + z}{2}$ .

Substituting these values into the given inequality $b + c \geq 2a$ gives $(y^2 - 1) + (z^2 - 1) \geq 2(x^2 - 1)$ , which simplifies to $y^2 + z^2 \geq 2x^2$ , and substituting $x = \frac{y + z}{2}$ into this gives $y^2 + z^2 \geq 2(\frac{y + z}{2})^2$ which rearranges to $(y - z)^2 \geq 0$ , which is always true for real numbers $y$ and $z$ .

Consider the function $f(x) = \sqrt{1 + x}$ . The statement given is equivalent to

$\frac{f(b) + f(c)}{2} = f(a)$ . We are asked whether this implies that $\frac{b + c}{2} \geq a$ .

Clearly this is true for the trivial case when $a=b=c$ . Let us assume $b \neq c$ .

Some things to consider about $f(x) = (1+x)^{\frac{1}{2}}$

• Its domain is $[-1,\infty)$

• Its first derivative is $f'(x) = \frac{1}{2} (1+x)^{\frac{-1}{2}}$ and $f'(x) > 0$ , for all $x \in (-1,\infty)$ . Thus $f(x)$ is an increasing function.

• Its second derivative is $f''(x) = \frac{-1}{4} (1+x)^{\frac{-3}{2}}$ and $f''(x) < 0$ , for all $x \in (-1,\infty)$ . Thus $f(x)$ is concave down.

In particular, for $b \neq c$ ,

$\frac{f(b) + f(c)}{2} < f(\frac{b+c}{2})$ . Thus $f(a) < f(\frac{b+c}{2})$ .

Since $f(x)$ is an increasing function over its entire domain, the latter fact implies that $a < \frac{b+c}{2}$ . QED

I write a python program to vividly showing the function and the relationship between a,b,c

import numpy as np
import matplotlib.pyplot as plt  
import math 

xLine = np.linspace(-1, 5, num=200)
y = np.array([ math.pow(item+1, 0.5) for item in xLine]) 

plt.plot(xLine,y,label='y = (x+1)^0.5')
plt.plot(xLine,xLine , label='y = x' )
plt.plot([-1, 1], [0, 2**0.5], 'ro', label= 'b,c')
plt.plot([-1/2], [0.5**0.5], 'go', label='a')
plt.legend()
plt.grid()
plt.xlabel('x')
plt.show()

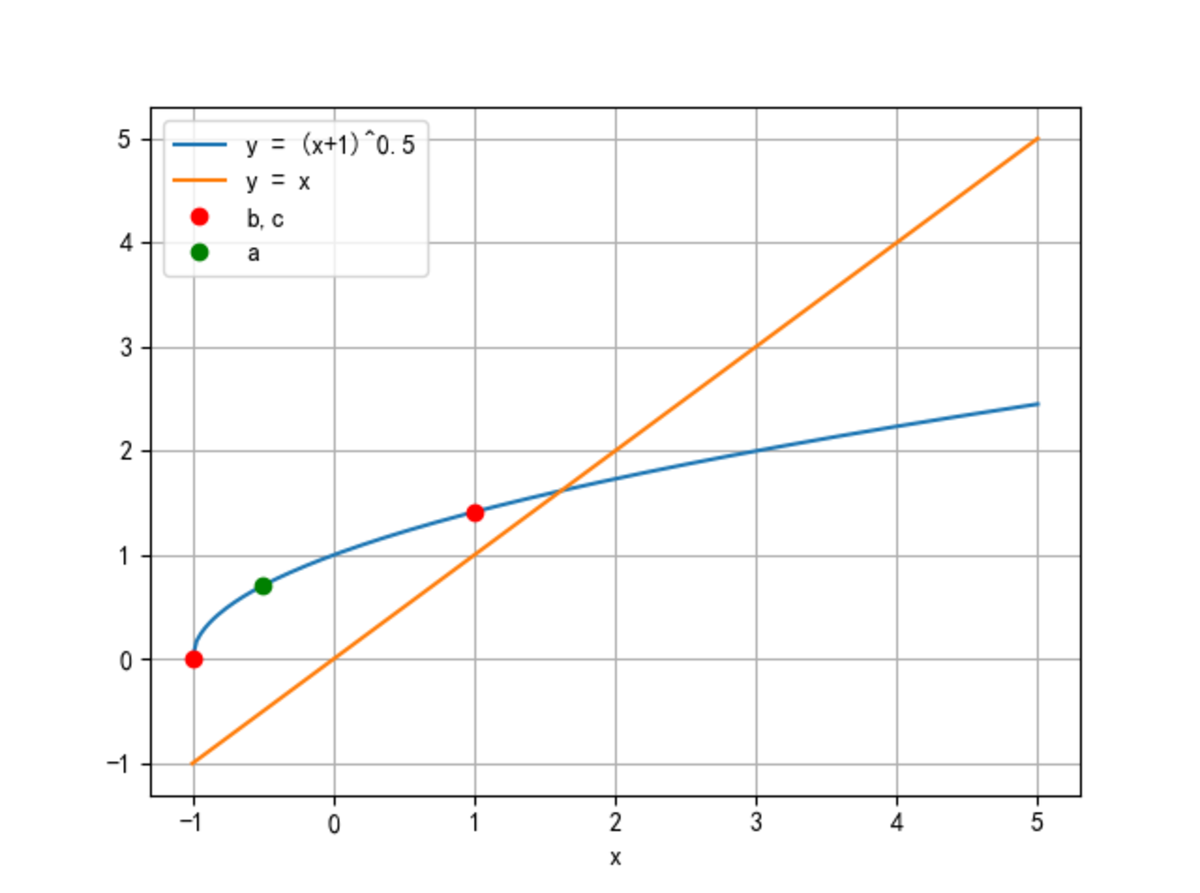
y = (1+x)^0.5 is a Convex function, so the inequality is always true