Sriking the support
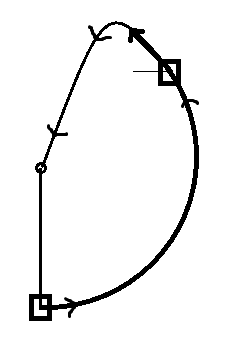 A block of mass 0.1 kg is tied to one end of a light string of length 0.1m whose other end is fixed to a rigid support as shown in the figure. The block is given a speed v from the lower most position such that
. When the block just leaves the circle the string is cut and the block moves as a projectile in a parabolic path and strikes the rigid support to which the string was attached. Find
if v=
where
is an acute angle in degrees.
A block of mass 0.1 kg is tied to one end of a light string of length 0.1m whose other end is fixed to a rigid support as shown in the figure. The block is given a speed v from the lower most position such that
. When the block just leaves the circle the string is cut and the block moves as a projectile in a parabolic path and strikes the rigid support to which the string was attached. Find
if v=
where
is an acute angle in degrees.
This problem is originally part of set Mechanics problems by Abhishek Sharma .
Try more problems here .
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As at point A tension is equal to 0,
m g c o s θ = l m v 2
Using conservation of energy,
2 1 m ( u 2 − c o s θ ) = m g ( l ( 1 + c o s θ ) )
Solving it we get,
c o s θ = 3 u 2 − 2
Now we form two equations using 2nd equation of motion and eliminate t to get,
tan 2 θ = 2
cos 2 θ = 3 1
Now replace cos θ with the value which we obtained earlier to get,
u = 2 + 3
α = tan − 1 2 + 3
α = 7 5 °