Vertical Circle
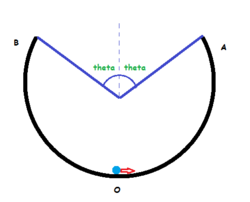 A wire is shaped in form of circular arc of a fixed radius as shown in the figure (
). A small mass is given horizontal velocity
from point
O
such that it travels on this smooth wire and reaches point
A
and then travels in the air to reach point
B
. Find the value of
such that
is minimum.
A wire is shaped in form of circular arc of a fixed radius as shown in the figure (
). A small mass is given horizontal velocity
from point
O
such that it travels on this smooth wire and reaches point
A
and then travels in the air to reach point
B
. Find the value of
such that
is minimum.
If can be represented as , select .
This problem is originally part of set Mechanics problems by Abhishek Sharma .
Try more problems here .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Applying work energy theorem at bottom most point and point of projection
2 1 m ( v ′ 2 − v 0 2 ) v ′ 2 2 R sin θ v ′ 2 v 0 2 − 2 g R ( 1 + cos θ ) 2 v 0 d θ d v 0 − 2 g R sin θ + g R sec θ tan θ cos θ = − m g R ( 1 + cos θ ) = v 0 2 − 2 g R ( 1 + cos θ ) = g v ′ 2 sin 2 θ = g R sec θ = g R sec θ = − 2 g R sin θ + g R sec θ tan θ = 0 [ ∵ d θ d v 0 = 0 ] = 2 1 θ = 4 π