Vertices and angles
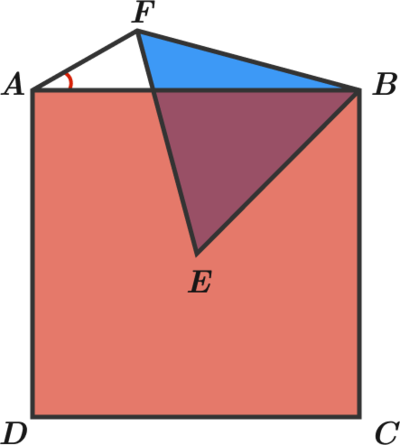
A B C D is a square and E is its center. F is chosen in order to create an equilateral triangle with B and E . What is the measure (in degrees) of ∠ F A B ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
@Brian Charlesworth okay, Thank you!
I like your solution, but I didn't understand who M is, don't you mean P?
Log in to reply
Sorry, yes, for some reason I typed P when I intended to type M . I've made the edit so that the point is consistently M now. :)
Nice question, by the way. I started off chasing angles until I realized I could look at it as a question on circles rather than squares. There are a couple of other ways of solving for ∠ F A B still using the circle approach, but the one I posted was the shortest.
@Brian Charlesworth I solved it by chasing angles, I really like when someone posts a solution that is different than mine.
@Brian Charlesworth How did you put the final answer (30 degrees) within a rectangle?
Log in to reply
Within the Latex bracketing, you type \boxed{30^{\circ}}, (where the ^{\circ} gives the degree notation). If you want to see how something is coded in Latex you can click on the three-dot icon at the lower-right corner of the question box and then choose the "Toggle LaTeX" option. To switch back after viewing the Latex coding you just choose "Toggle LaTeX" again.
As we should know, any square can be inscribed inside a circle, in this case, of center in E . Here E F ≅ E D are radii of the circle and, therefore ∠ B A F is inscribed in the circle, enclosing the same arc as ∠ B E F , then: ∠ B E F = 2 ⋅ ∠ B A F ⇒ ∠ B A F = 3 0 ∘
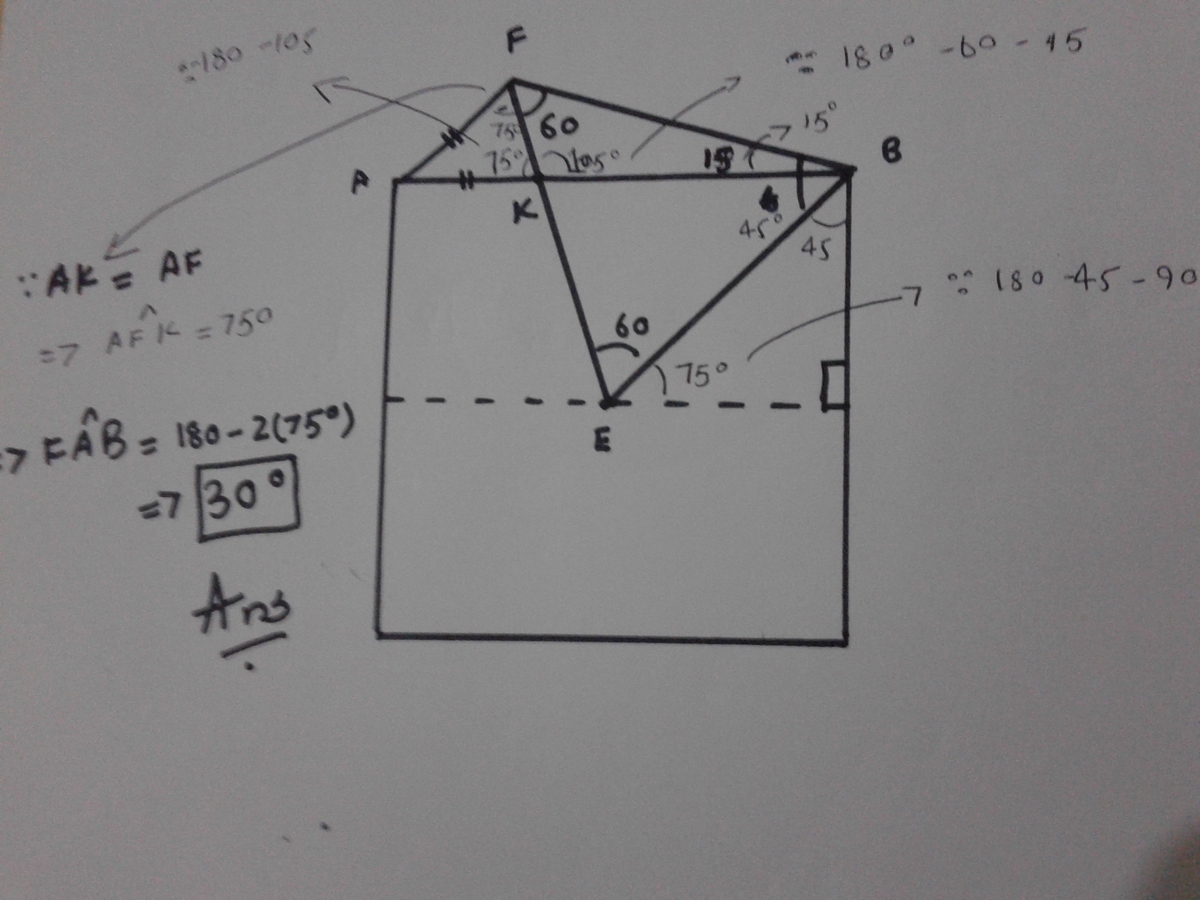
Extend BF and EA, so that these two lines meet at a point G.FE=BE=AE, so we have isosceles triangle AFE. Angle EAF= 75, so angle FAB=30.
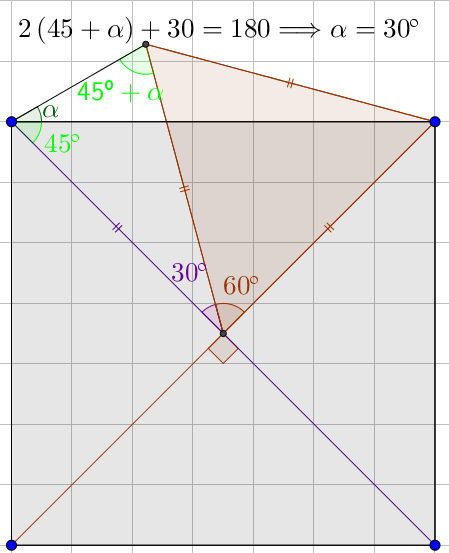
Points A , B , C , D and F all lie on a circle with center E . As ∠ F A B and ∠ F E B are subtended by the same chord F B we then know from our knowledge of inscribed angles that
∠ F A B = 2 1 ∠ F E B = 2 1 × 6 0 ∘ = 3 0 ∘ .
Comment: Let M be the point of intersection of A B and E F . As ∠ E B M = 4 5 ∘ we have that ∠ A M F = ∠ E M B = 7 5 ∘ , and so as ∠ F A B = 3 0 ∘ we have that ∠ A M F = 7 5 ∘ as well. Thus Δ A M F is isosceles, which I thought was an outcome worth noting.