Circle problem
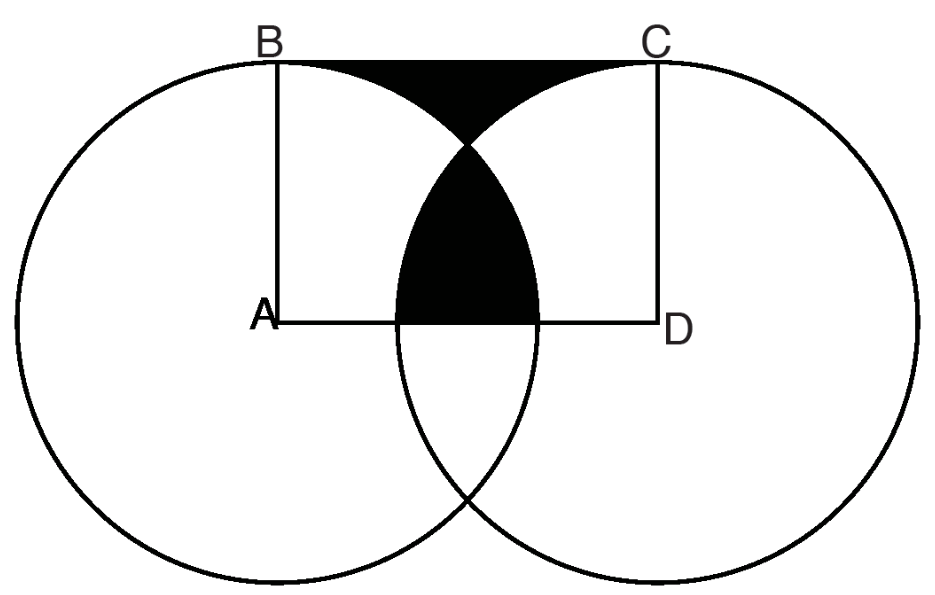
In the above diagram, A B and D C are radii of circles A and D with length 1. If ABCD is a rectangle, find its area.
Use the approximation π = 3 . 1 4 and answer to two decimal places.
Credit: New York Math League Contest
The answer is 1.57.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
There's a direct immediate way to conclude that the area is 2 π .
Hint: The area of a quarter circle is ...
Log in to reply
Arghhh.... How did I miss the easy way. :( Since the region of overlap of the two quarter-circles has the same area as the upper shaded region, the area of A B C D is just the sum of the areas of two quarter-circles, i.e., the area of a half-circle, which with the radius being 1 is simply 2 π .
I like how you used calculus though it was totally unnecessary :)
Log in to reply
Yeah, I know. .... f a c e p a l m ... I forgot the cardinal rule of problem solving: THINK first, and resort to calculus only when absolutely necessary.
An interesting follow-up question is this: if the area of the upper shaded region is n times that of the lower shaded region, (where n ≥ 0 is a real number) , then what is the area of A B C D ?
Log in to reply
I just had a chance to work on my follow-up question. This time calculus was necessary. The area a would be the solution of the equation
a + ( n − 1 ) arcsin ( 2 a ) + ( n − 1 ) ( 2 a ) 1 − 4 a 2 = 2 n π .
For n = 1 we would get a = 2 π as before, and for n = 0 we would get a = 0 , as expected. Also, in the limit as n → ∞ we would get a → 2 , again as expected. (This would correspond to the circles being tangent to one another, making A D = 2 ).
For any other value of n we would have to rely on numerical methods, (i.e., WolframAlpha, etc.), to solve for a . For n = 2 we would then get a = 1 . 6 8 5 5 . . . , and for n = 3 we would have a = 1 . 7 4 2 . . . . .
I like that idea!
.#problemswithbeingtoosmart haha XD.
the area would be sum of two quarters and the upper shaded region...but due to overlapping of the quarters, the lower shaded portion needs to be deducted...so area= sum of two quarters(( 3.14 /2 ) since radius is 1) + upper shaded region - lower shaded region...as the areas of shaded regions are equal so we are finally left with the area of the two quarters.
The area of each quarter of the circles added together is (Pi/4) * 2=Pi/2. This includes a double counting of the shaded area inside the circles, but that double counting exactly equals the shaded area outside the circles as given in the instructions. So the area of the quadrilateral is just Pi/2 = 1.57.
Let x be the area of one shaded region. By analyzing the geometry, We can say that, Area of Quadrilateral ABCD is = Pi/4 +Pi/4 (Quarter of a unit circle - whole circle area = Pi as radius is 1) -x(subtract the area of intersection)+x (add area of above intersection which is same as x)=Pi/2=1.57
It is assumed that A B ∣ ∣ C D .
Let A be the origin and A D = a lie on the positive x -axis. The circle on the left then has equation x 2 + y 2 = 1 and the circle on the right has equation ( x − a ) 2 + y 2 = 1 . The uppermost point of intersection of the two circles lies at ( 2 a , 1 − ( 2 a ) 2 ) .
The area of the upper shaded region will then be
2 ∗ ∫ 0 2 a ( 1 − 1 − x 2 ) d x ,
and the area of the lower shaded region will be
2 ∗ ∫ 2 a 1 1 − x 2 d x .
For these two areas to be equal we must then have that
∫ 0 2 a ( 1 − 1 − x 2 ) d x = ∫ 2 a 1 1 − x 2 d x
⟹ ∫ 0 2 a d x = ∫ 0 1 1 − x 2 d x ⟹ 2 a = 4 π ⟹ a = 2 π .
So the area of quadrilateral A B C D is A B ∗ A D = 1 ∗ a = 2 π = 1 . 5 7
to 2 decimal places.