This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
It is an equation in one variable, simple. . .
Which means?
2x^2001+3x^2000+.............................. + 2x+3=0 x^2000(2x+3)+x^1998(2x+3)+........................+ 1(2x+3)=0 (x^2000+x^1998+............................+x^2+1)(2x+3)=0 ONE ROOT : x=-3/2 x^2000+x^1998+.......................+ x^2=-1 Sum of positive integers is always greater than or equal to zero. therefore only one real root.
x 2 is not necessarily an integer, it is a real number. It is not necessarily positive, it is nonnegative. A positive number cannot be 0.
Grouping the even and odd exponents:
2 i = 0 ∑ 1 0 0 0 x 2 i + 1 + 3 i = 0 ∑ 1 0 0 0 x 2 i = 0
Because x a + b = x a x b , an x is factored from the odd exponents:
2 x i = 0 ∑ 1 0 0 0 x 2 i = − 3 i = 0 ∑ 1 0 0 0 x 2 i
Because x = 0 is not a solution to the original equation, ∑ x 2 i is non-zero. Dividing each side by it yields:
2 x = − 3
So x = − 3 / 2 , the only root.
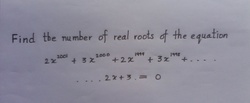
The equation can be factored as:
( 2 x + 3 ) ( 1 + x 2 + x 4 + x 6 + . . . + x 2 0 0 0 ) = 0
0nly one factor gives a real root.