Very Small Physics 3
The founders of quantum mechanics largely ignored relativity when they first applied quantum theory to chemistry:
"The general theory of quantum mechanics is now almost complete... they give rise to difficulties only when high-speed particles are involved, and are therefore of no importance in the consideration of atomic and molecular structure and ordinary chemical reactions." - Paul Dirac, 1929
Treat an atom as a two-body problem with one electron and a central nucleus with a charge Z and a mass much greater than the electron.
Was Dirac correct? At what element in the periodic table would relativistic effects become important for an electron in a ground state?
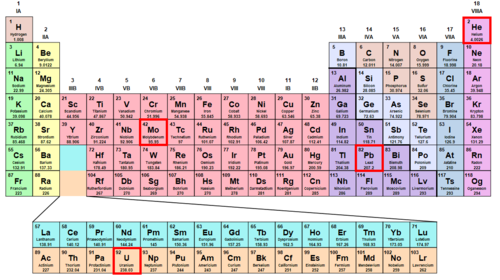
Note: Significant errors start to appear between classical and relativistic dynamics when the Lorentz factor γ = 1 − v 2 / c 2 1 ≥ 1 . 0 5 . It may be useful to perform this calculation in atomic units , where ℏ , e , m e , and 4 π ϵ 0 are defined as 1 . In these units, the speed of light is c = 1 3 7 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
In the last line of your solution, you accidentally put a decimal point in your value for c, just so you know.
Wait ... it does not make sense. If you invoke the ground state of the electron, why don't you get the velocity? Of course the velocity would not depend on Z anymore.
Without that invoking it, I got v^2=Z instead of v=Z. Then there is no solution!
Sorry, the invoked equation is all about removing r. That is fine.
The run down
In the second Very Small Physics problem, we treated an atom as a two-body problem and found the radius of the ground state of hydrogen. In this problem we'll do something similar, but allow the charge on the nucleus Z to vary. Then we'll find the kinetic energy associated with the ground state electron, and find it's velocity. When the charge Z gets higher than 42, the velocity of the ground state electron becomes greater than 3 0 % of the speed of light and results in a Lorentz correction γ > 1 . 0 5 .
Total Energy
As we did in the Intermediate problem, we set up the total energy of an electron with a confinement energy. This energy was yielded by making an approximation for the coupling of momentum and position in a quantum mechanical electron according to the uncertainty principle: r p ∼ ℏ . This time we'll allow the charge in the nucleus to vary, and so there is a factor of Z in the Coulombic term.
E t o t = 2 m p 2 − 4 π ϵ 0 r Z e 2 = 2 m r 2 ℏ 2 − 4 π ϵ 0 r e 2
This simplifies greatly if we use atomic units , a great suggestion by @Mark Hennings :
E t o t = 2 r 2 1 − r 1
We can now see that the kinetic and potential energies are coupled , and both depend on the electron-nucleus separation. The confinement energy approaches positive infinity much faster than the Coulombic energy approaches negative infinity as the radius goes to zero. The expected radius of an electron can be found by minimizing this energy:
d r d E r 3 1 r = r 3 − 1 + r 2 Z = 0 = r 2 Z = Z 1
By using our uncertainty principle approximation, the momentum of the electron at this expected radius is given by:
p = r 1 = Z
The "velocity" of the electron is just this momentum divided by the mass of the electron ( m e = 1 in atomic units).
v = m e ∣ p ∣ = Z
In Hydrogen ( Z = 1 ) the electron isn't even close to relativistic. A velocity of v = 1 is about 137th the speed of light in these units. We can calculate the Lorentz factor for this Hydrogen ground state electron without using any physical constants other than c = 1 3 7 in atomic units:
γ = s q r t 1 − Z 2 / c 2 1 = 1 . 0 0 0 0 2 6 6
This is a tiny relativistic correction.
To reach a Lorentz factor of γ = 1 . 0 5 , we need v / c = 0 . 3 , or 3 0 % the speed of light. Based on the linear relation between velocity and charge Z , we just need 0 . 3 / 0 . 0 0 7 3 = 4 1 . 1 times the charge. The element with an atomic number of 4 2 is Molybdenum. In atomic units this calculation is even easier:
c Z = 1 3 7 Z ≥ 0 . 3
So again the minimum charge is Z = 4 2 .
For elements larger than Molybdenum, relativistic effects begin to significantly change the orbits of the electrons. These effects are possibly most well known for the color of gold (element 79, Au). In Gold, not only are the ground state orbits relativistic, but so is the highest occupied orbital, 6 s . Electrons in 6 s are traveling so fast that their increased relativistic weight leads to a contracted orbital radius and a lower energy.
This narrows the energy gap between the two highest orbitals 5 d and 6 s . In lower Z elements of the same period (like Silver), this gap ( 4 d → 5 s ) is wide enough that only UV light can excite electrons up to this state. So silver absorbs UV but reflects the entire visible spectrum, resulting in a white coloring. In gold, the narrowed gap can be excited with blue light, and so gold absorbs blue but reflects the rest of the visible spectrum. We perceive this color as yellow.

Plugging in the constants into the velocity equation, doesn't the velocity of a hydrogen atom at Z = 1 come to 2 . 1 8 8 × 1 0 6 ms − 1 ?
Log in to reply
You are absolutely correct. Must have had a calculator typo somewhere. Thanks David!
I generally don't care for the physics problems because they are like easy math problems with hidden information. But I take a stab at them and can sometimes get the answer. The following solution took some lucky guesses.
I took a hint from an intermediate problem for this week. Plugging all the 'atomic units' into the solution formula gives a radius of 1. That's from having a +1 in the nucleus. What happens if we crank it up? Faster electron. How much faster?
The two body problem link gives v = r G M . I figured the M and r can't change so v is probably proportional to G . G is usually a gravitational force, maybe here it can be substituted for the charge of the nucleus.
Solving the γ formula gives v ≥ 4 1 . 7 7 Molybdenum is #42. That can't be a coincidence.
Something is slightly wrong, though, because it looks like v is actually proportion to G . Or I made some other mistake. I don't really care. Back to the math problems, where everything is laid out.
Hey Jeremy-
Very enterprising approach you took, even though it's a physics problem.
If you assume that G can be substituted for Z in the two body problem equation, you end up v = Z . Then with the Lorentz factor formula:
1 − v 2 / c 2 1 1 − v 2 / c 2 1 − v 2 / c 2 v 2 / c 2 v 2 ≥ 1 . 0 5 ≥ 0 . 9 5 2 ≥ 0 . 9 0 6 3 ≥ 0 . 0 9 3 7 ≥ 0 . 0 9 3 7 c 2
Substituting in v = Z and c = 1 3 7 : Z ≥ 1 7 5 8 . 6 5
Which is far too large and wouldn't ever yield the correct answer of 4 2 . While a classical two body problem (like a gravitational orbit) has an infinite number of possible stable orbital radii, the coupling between momentum and radius given by the uncertainty bound creates a minimum orbital radius for a quantum object. Finding this minimum (by setting the derivative of the two body energy formula to zero) yields the correct dependency on Z in atomic units:
v = Z
So substituting this in the formula we got above:
Z 2 ≥ 1 7 5 8 . 6 5 Z ≈ 4 2 .
I don't know much about physics, but Uranium, Lead and Helium are all elements people talk about. You never hear about Molybdenum. The only reason it could be one of the answer choices would be if it was the correct answer. Although not always effective, tapping into human psychology can help improve the odds of a random guess.
Treating the set-up as a classical two-body problem, the electrostatic attraction between the nucleus and the electron must provide the necessary centripetal acceleration, and so 4 π ε 0 r 2 Z e 2 = r m e v 2 o r m e v 2 r = 4 π ε 0 Z e 2 We are assuming that angular momentum is quantized, and that the electron is in the ground state. Thus we require m e v r = ℏ In both of these equations r is the radius of the electron's orbit, and v the electron's velocity. Thus v = 4 π ε 0 ℏ Z e 2 In atomic units, this means that v = Z , and hence that γ = ( 1 − c 2 Z 2 ) − 2 1 . Thus γ ≥ 1 . 0 5 when Z ≥ c 1 . 0 5 1 . 0 5 2 − 1 = 0 . 3 0 4 9 c With c ≈ 1 3 7 we deduce that Z ≥ 4 1 . 7 7 3 , and hence Z ≥ 4 2 , making M o l y b d e n u m the answer.