Vibration in Charged Particle

Electricity and Magnetism Level 3

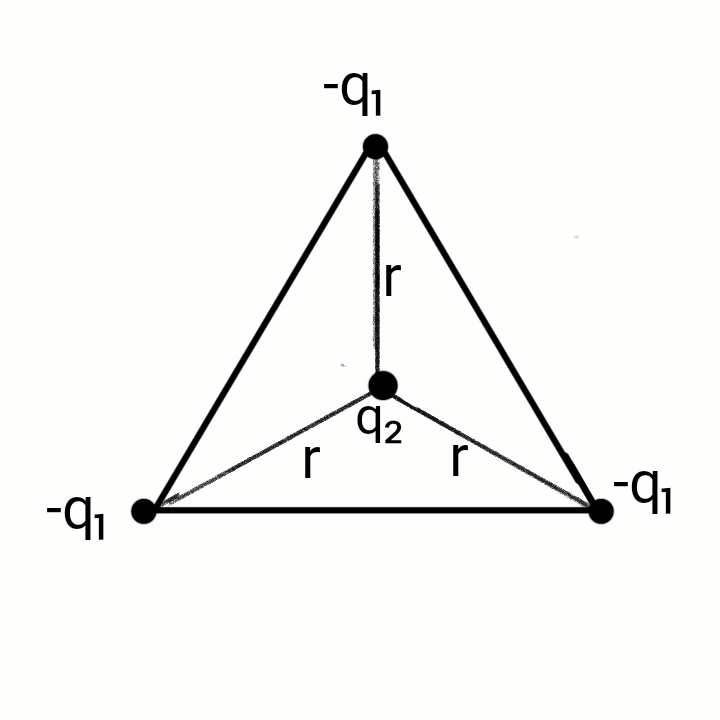
Three equal negative charges, - ${ q }_{ 1 }$ each, form the vertices of an equilateral triangle. A particle of mass m and a positive charge ${ q }_{ 2 }$ is constrained to move along a perpendicular to the plane and through it's center which is at a distance r from each of the negative charges as shown in the figure. The whole system is kept in gravity free space.

The time period of vibration of the particle for small distance from the equilibrium position can be expressed as

T = ${ A }{ \pi }\sqrt { \frac { { \pi }{ { { \varepsilon }_{ \circ } } }{ m }{ r }^{ B } }{ { C }{ q }_{ 1 }{ q }_{ 2 } } }$

then A+B+C equal to ?

The answer is 10.

1 solution

Steven Chase
Mar 23, 2018

Differential equation for motion:

$-\frac{3 \, q_1 q_2 \, y}{4 \pi \epsilon_0 (r^2 + y^2)^{3/2}} = m \ddot{y}$

Approximation for small $y$ :

$-\frac{3 \, q_1 q_2 \, y}{4 \pi \epsilon_0 r^3} = m \ddot{y} \\ -\frac{3 \, q_1 q_2}{4 \pi \, m \, \epsilon_0 r^3} y = \ddot{y}$

This corresponds to simple harmonic motion with the following angular frequency:

$\omega = \frac{2 \pi}{T} = \sqrt{\frac{3 \, q_1 q_2}{4 \pi \, m \, \epsilon_0 r^3}} \\ T = 2 \pi \, \sqrt{\frac{4 \pi \, m \, \epsilon_0 r^3}{3 \, q_1 q_2}} = 4 \pi \, \sqrt{\frac{\pi \, m \, \epsilon_0 r^3}{3 \, q_1 q_2}}$

Did the same sir

A Former Brilliant Member - 3 years, 2 months ago

Vibration in Charged Particle

The answer is 10.

1 solution

0 pending reports