Viscosity + Rotation combined
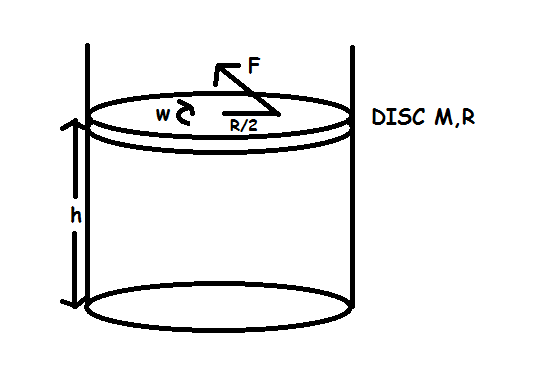
A cylindrical container of radius R has a cylindrical lid, with liquid filled up to height h.
The fluid has a coefficient of viscosity
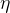 .
The lid has mass M and is rotated with angular velocity
.
The lid has mass M and is rotated with angular velocity
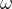 in clockwise sense as seen from top. At the same time a force F acts at a distance R/2 opposing the angular velocity.
in clockwise sense as seen from top. At the same time a force F acts at a distance R/2 opposing the angular velocity.
Find the time after which the lid comes momentarily to rest.
If the answer is of form
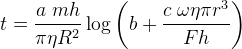 find a+b+c
find a+b+c
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Actually, the last equation has a typo.
Excellent Solution :)
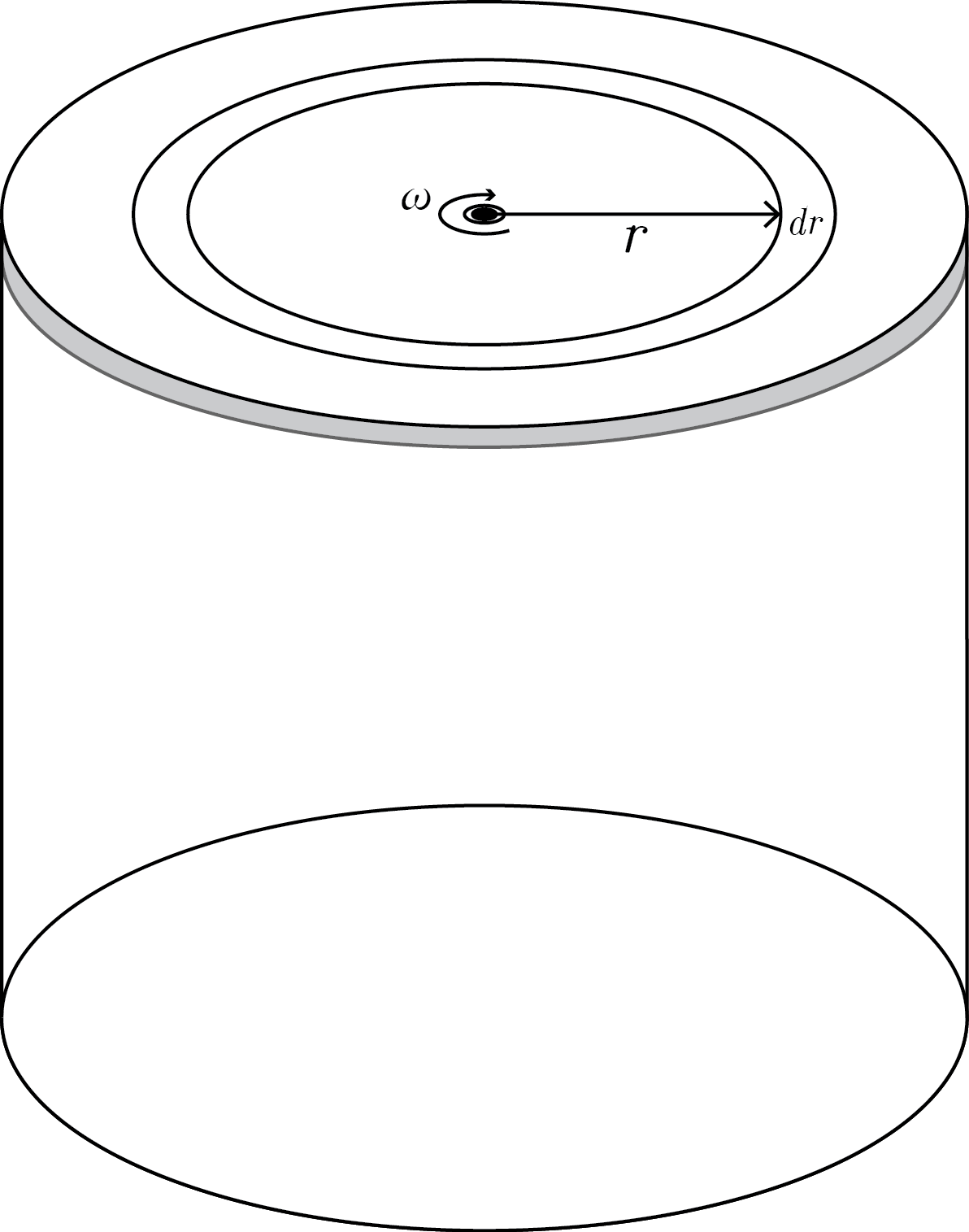
Let's write velocity of a small ring at a distance r from axis of rotation, v ( r ) = ω r
So, the velocity gradient at a distance r from axis of rotation becomes, d z d v = h v ( r ) = h ω r Force due to viscosity, F ( r ) = − η S d z d v = − η ⋅ 2 π r d r h ω r
So, the small torque acting due to viscosity, d τ 1 = r F ( r ) = − h 2 π η ω r 3 d r τ 1 = − h 2 π η ω ∫ 0 R r 3 d r = − 2 h π η ω R 4
Torque due to the external force is, τ 2 = − 2 F R
So, the net torque becomes, τ = τ 1 + τ 2 = − 2 R ( h π η ω R 3 + F )
Now, 2 1 M R 2 α = τ ⇒ α = − M R 1 ( h π η ω R 3 + F )
Integrating, t = M R ∫ 0 ω ( h π η ω R 3 + F ) 1 d ω = π η R 2 M h ln ( 1 + F h π η ω R 3 )
Thus, a + b + c = 3
Did the same, great question!!!
When a solid is moved in a liquid is suffers a viscous force which is given as F = η A Δ z Δ v Here, η is the coefficient of viscosity, A is the surface area and Δ z Δ v is the velocity gradient. The disc in the problem will also suffer a viscous force that will produce a torque to oppose the rotation of the disc.
The disc can be assumed to be made up of many thin circular rings. Imagine a ring of radius r(<R) and thickness dr. The points on the ring have speed r ω . The torque on this ring will be.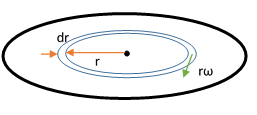
d τ = ( η 2 π r d r h r ω ) r The total torque on the disc due to viscous force can be calculated by integrating the torque ∫ 0 τ d τ = ∫ 0 R ( η 2 π r d r h r ω ) r τ = 4 h η 2 π ω R 4
The torque on the disc is also applied by the force F. τ = F 2 R The total torque equals τ = 4 h η 2 π ω R 4 + F 2 R
This torque creates an angular retardation ( α = − d t d ω ), and the torqe τ = I α Moment of inertia (I) of disc = 2 M R 2 Thus, we have 4 h η 2 π ω R 4 + F 2 R = − 2 M R 2 d t d ω ∫ 0 t 2 h M R d t = − ∫ ω 0 η 2 π ω R 4 + 2 F R d ω 2 h M R t = η 2 π R 4 ln ( 2 F R η 2 π ω R 4 + 2 F R ) t = η π R 4 M R h ln ( 1 + F R η π ω R 4 ) Comparing it with the form in the quesiton we will have a=1, b=1 and c=1 and therefore, a+b+c=3.