Viscous Trajectory

Classical Mechanics Level 4

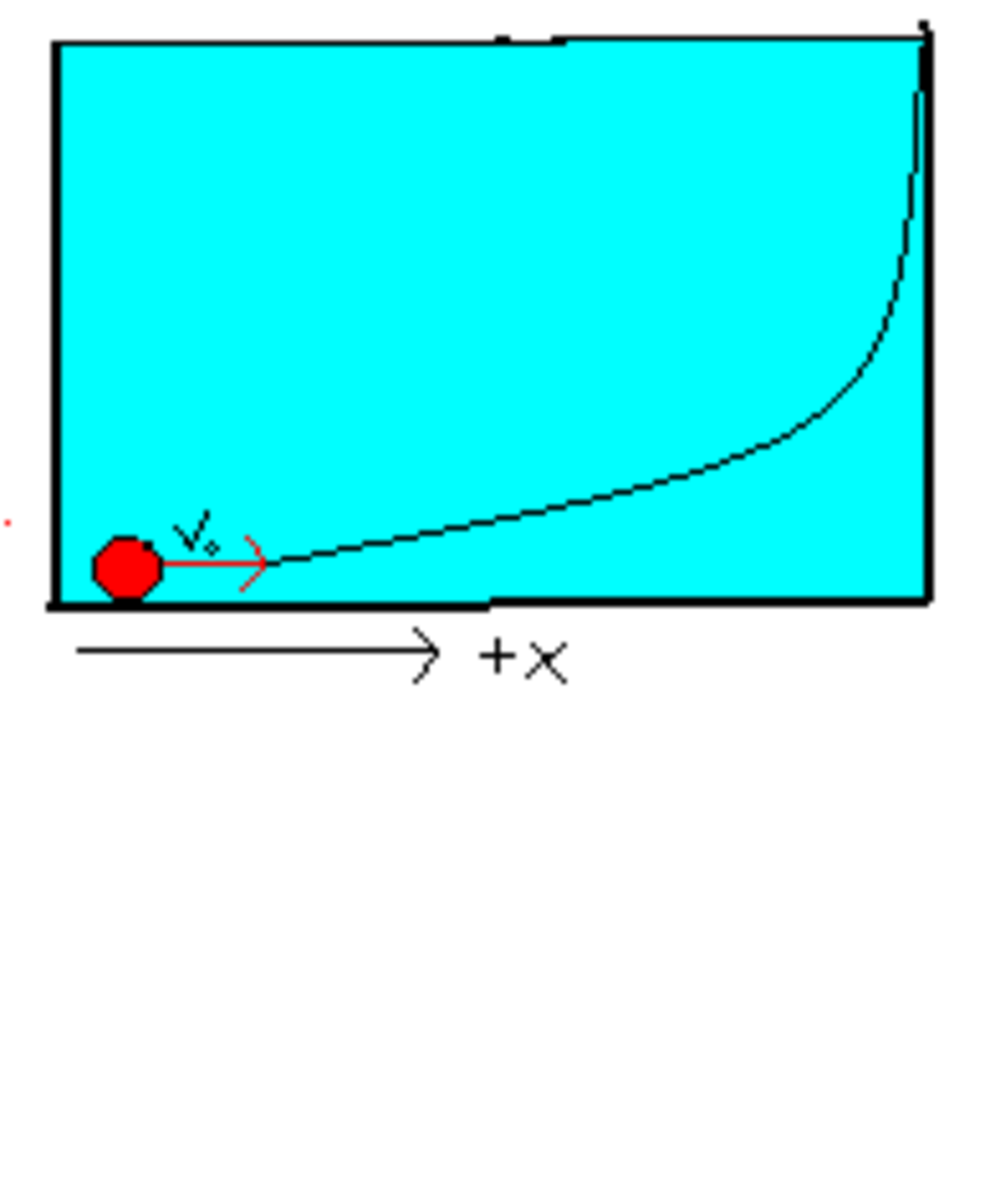
This problem was asked to a friend of mine in the KVPY interview. He was asked to describe the motion qualitatively. I wanted to analyze it quantitatively.

A solid wooden sphere with density less than water is released with a speed v in water, along the positive $x$ axis, at the origin.

Find its maximum $x$ coordinate (in meters)

Details and assumptions

Stoke's law is applicable.
The tank is very wide and very deep, so that the sphere loses all horizontal velocity before breaching the surface.
Mass of the sphere = $\SI{6}{\kilo\gram}$ .
Initial speed = $\SI{\pi}{\meter/\second}$ .
Radius of sphere = $\SI{0.5}{\meter}$ .
Coefficient of viscosity = 1.

The answer is 2.0.

1 solution

Pinak Wadikar
May 6, 2014

6 $\pi$ nrv = mv $\frac{dv}{dx}$

$6 \pi nr \times dx = m \times dv$

solving the differential we get $m ( v - v' ) = 6 ( \pi$ nrx ) {1}

Here:

v: Final Velocity
v': Initial velocity
x: displacement at that instant

The ball will be at its maximum x coordinate when velocity in that direction will tend to zero.
Form an equation of x in terms of v {eqn 1}
take limit v tends to zero.

you will get answer $\boxed{2}$

“The ball will be at its maximum x coordinate when velocity will tend to zero"?

Don't you mean when the x component of its velocity will be zero? It will have vertical component due to buoyant force.

Siddharth Brahmbhatt - 6 years, 12 months ago

I think he meant the same.

Ankit Kumar Jain - 3 years, 1 month ago

Viscous Trajectory

The answer is 2.0.

1 solution

0 pending reports