Visual Prediction
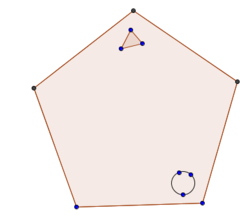 The circle moves two places anti-clockwise at each stage and the triangle moves one place clockwise at each stage. After how many stages will they be together in the same corner?
The circle moves two places anti-clockwise at each stage and the triangle moves one place clockwise at each stage. After how many stages will they be together in the same corner?
Note : Moving one places signifies moving one corner.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
This made sense to me, I was completely stumped. 👏👏
reletive, this is like physics
I also know
why is this hard?!!
later tell me how do you solve this.
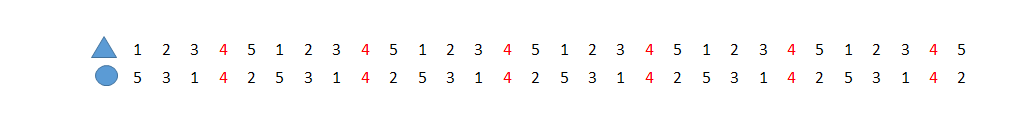
When the circle moves two places anti-clockwise at each stage and the triangle moves one place clockwise at each stage they always meet at vertex 4 in every four stages.
Or you could just try getting the circle to the triangle because the circle and the triangle lets say are at points A and C and also it sorta looks like the point are equal by moving the circle enough the corner won't get too close to the triangle. Boom another theory
stupid, awsome brilliant.org supports you, subscribe to pewdiepie and help youtube live
Yes, this is how I did it...
............
The movements can be represented using modular arithmetic as follows: ( + 1 ) x ≡ 0 m o d ( 5 ) , ( − 2 ) y ≡ 2 m o d ( 5 ) Where the numbers in the brackets represent the movements after each step. If a represents the number of movements such that the triangle and circle end up in the same position then: y − 2 a ≡ ( x + a ) m o d ( 5 ) ⇒ 2 ≡ 3 a ⇒ 1 2 ≡ 3 a ⇒ 4 ≡ a Testing this out find that they do indeed end up at the same vertex after 4 moves.
What is modular arithmetic ; .I had to count the moves to come up with the answer. Yours is more sophisticated
The idea of using modulo operation seems fine, but I'm not sure if second line of implications is correct
relative velocity between the triangle and the circle = 3 places/stage Distance between the shapes = 2 , 7, 12, 17, 22, ... (each loop around the pentagon would consist of 5 places, so adding 5 places per loop)
12 is the minimum distance that is divisible by the velocity i.e., 3
Therefore, number of stages required = 12/3 = 4
I'd just point with my fingers.
"fascinating"
Suppose, at present triangle is at corner 1 & circle is at corner 3 ( named the corners 1, 2, 3, 4 & 5 clockwise direction ). At 1st stage triangle comes to at corner 2 and in this way at 4th stage triangle comes to at corner 5, likewise at 1st stage circle comes to at corner 1 (move anticlockwise from corner 3 to on 1) and in this way at 4th stage it get co-inside with triangle at corner 4 ( Ans.)
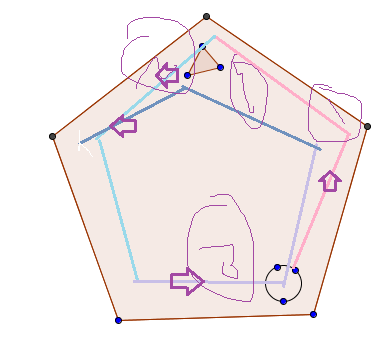
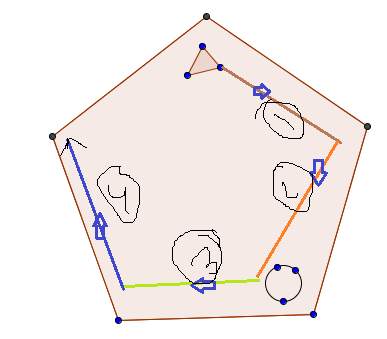
Relative to the triangle, the circle moves three places counterclockwise in each move. A simple count, keeping the triangle fixed, shows that four moves are required.