Viviani or not

Geometry Level 4

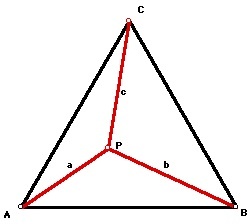
A point $P$ is found inside equilateral triangle $ABC$ such that its distance from the vertices are 5, 6 and 7 in any order. If the area enclosed by $\Delta ABC$ amounts to $r + s\sqrt{t}$ unit triangles, where $r$ , $s$ , and $t$ are positive integers and $t$ is square free, find $r+s+t$ .

Note:

A unit triangle is the area of an equilateral triangle whose side length is one unit.

The answer is 93.

2 solutions

Ahmad Saad
Mar 28, 2017

Efren Medallo
Mar 24, 2017

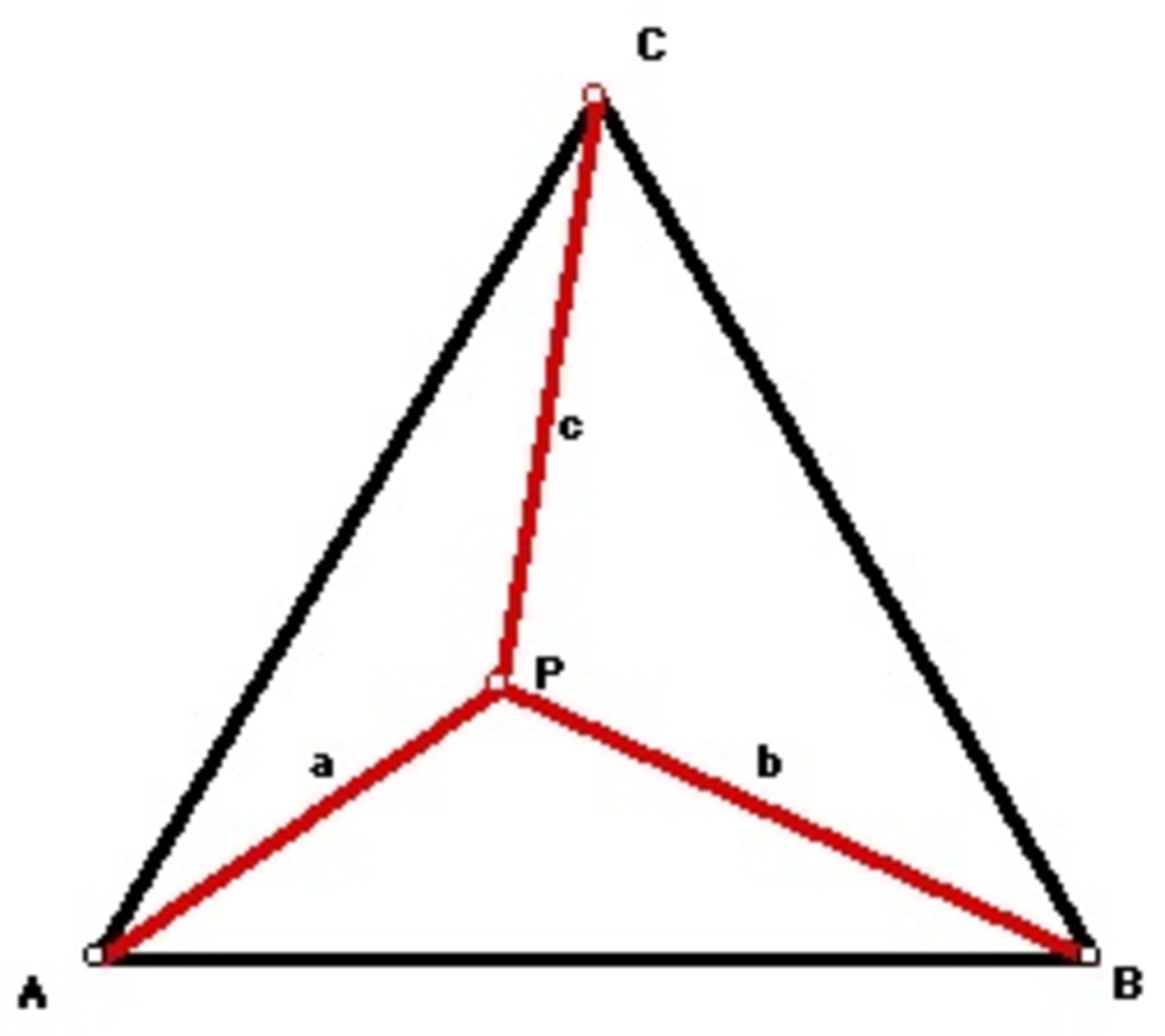
Let us visualize the problem in this figure. Assuming that a=5, b=6, and c=7, we now have to find the area of triangle ABC.

At first look, we may be tempted to use Viviani’s Theorem to solve this problem, but such is not the case as the segments emanating from the point P end at the vertices of the triangles.

Acknowledging that, one might be tempted to use the cosine law, with which you will have three equations with four unknowns (3 angles and the side length). Add to that the fact that the three unknown angles around P add up to 360 degrees, we have four equations with four unknowns.

That is tedious, messy, and involves a lot of unnecessary work (i.e., determining the angles which are essentially not needed).

However, we can use Heron’s formula to directly solve for the side length, and later, the area. Sure, it may be also prove tedious, but at least it is a little more straighforward.

$A = \sqrt{s(s-a)(s-b)(s-c)}$

where $s$ is the half the perimeter of the triangle, and $a, b,$ and $c$ are its sides.

Let the side length of the triangle be $N$ .

Let the lengths $a, b,$ and $c$ be $5, 6,$ and $7$ , respectively.From the figure, we can derive that $A_{APB} + A_{BPC} + A_{APC} = A_{ABC}$

Individually finding solving for these areas, we can see that they can all be expressed in terms of $N$ .

$A_{APB} = \sqrt{s(s-5)(s-6)(s-N)}$

and $s= \frac{5+6+N}{2} = \frac{11+N}{2}$

simplifying further, we will get $A_{APB} = \frac{1}{4}\sqrt{(121-N^2)(N^2-1)}$ In a similar manner, we will get the following:

$A_{BPC} = \frac{1}{4}\sqrt{(169-N^2)(N^2-1)}$

$A_{APC} = \frac{1}{4}\sqrt{(144-N^2)(N^2-4)}$ Now, we add these all and equate this to this equation: $A_{ABC} = \frac{N^2 \sqrt{3}}{4}$ knowing that this triangle is equilateral. Now, we equate this to the sum of those three sub areas and we get an equation in N. There is no easy way to solve this equation, you may do it graphically, or do it via approximations. When plugged on W|A, it is revealed that the answer is

$N= \sqrt{55+36\sqrt{2}}$

since the length of the triangle is $N$ , then its area is equal to $N^2$ unit triangles.

Thus we arrive at the answer: $\boxed{55+36+2 = 93}$ .

Viviani or not

The answer is 93.

2 solutions

0 pending reports