Volcanic Sangaku
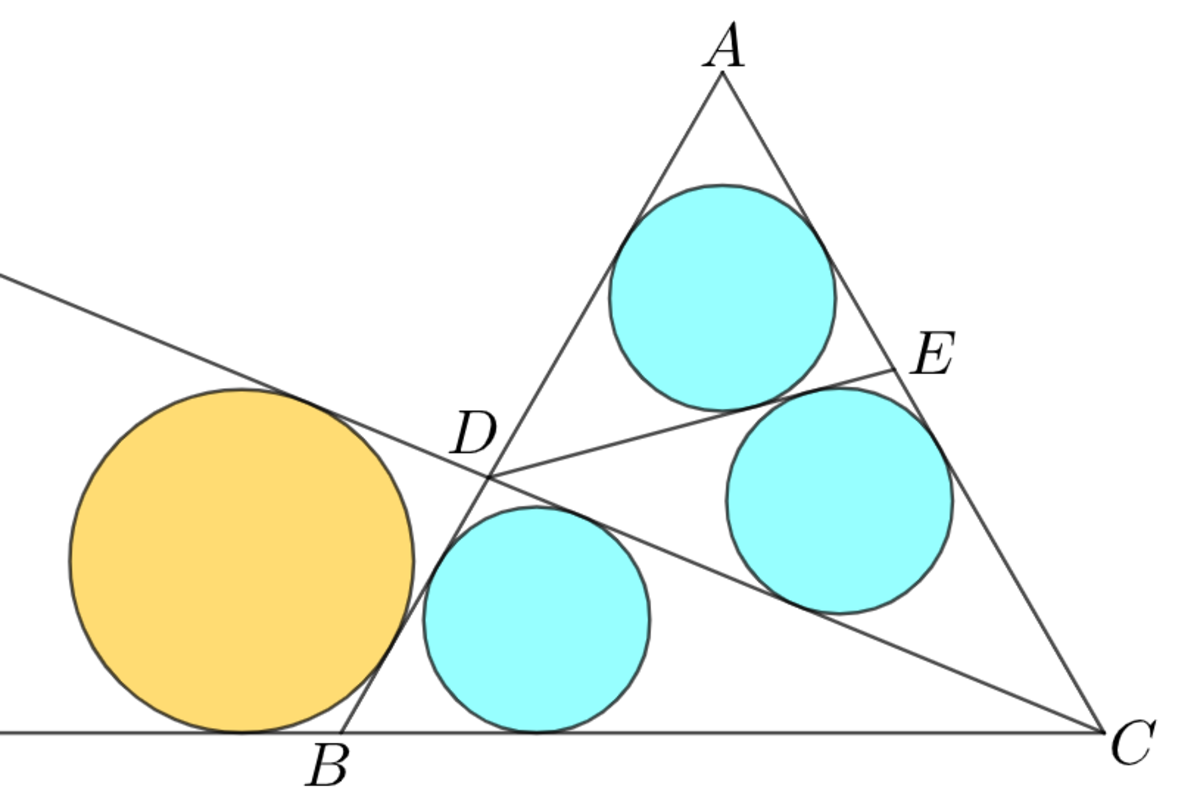
In the equilateral triangle , points and are selected, such that:
- and form three identical cyan incircles;
- And that two segments are extended indefinitely from to form an orange circle tangent to .
If the ratio of the radius of the orange circle to the radius of one cyan circle can be expressed as , where are positive integers, coprime and square free, input the product as your answer.
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the sides of the equilateral triangle be 1 , and let p = B D , q = C E , t = D E , and u = C D .
The area of △ B C D is T △ B C D = 2 1 ⋅ p ⋅ 1 ⋅ sin 6 0 ° = 4 3 p , and the semiperimeter of △ B C D is s △ B C D = 2 1 ( p + u + 1 ) .
The area of △ A D E is T △ A D E = 2 1 ⋅ ( 1 − p ) ⋅ ( 1 − q ) ⋅ sin 6 0 ° = 4 3 ( 1 − p ) ( 1 − q ) , and the semiperimeter of △ A D E is s △ A D E = 2 1 ( 2 − p − q + t ) .
The area of △ E D C is T △ E D C = T △ A B C − T △ B C D − T △ A D E = 4 3 − 4 3 p − 4 3 ( 1 − p ) ( 1 − q ) = 4 3 ( 1 − p ) q , and the semiperimeter of △ E D C is s △ E D C = 2 1 ( t + u + q ) .
Since the inradius is r = s T and each incircle is equal,
r = 2 1 ( p + s + 1 ) 4 3 p = 2 1 ( 2 − p − q + t ) 4 3 ( 1 − p ) ( 1 − q ) = 2 1 ( t + u + q ) 4 3 ( 1 − p ) q
By the law of cosines on △ B C D , u = p 2 + 1 2 − 2 ⋅ p ⋅ 1 cos 6 0 ° , or
u = p 2 − p − 1
and by the law of cosines on △ A D E , t = ( 1 − p ) 2 + ( 1 − q ) 2 − 2 ⋅ ( 1 − p ) ⋅ ( 1 − q ) cos 6 0 ° , or
t = p 2 + q 2 − p q − p − q + 1
Substituting u and t into the inradius equations 2 1 ( p + u + 1 ) 4 3 p = 2 1 ( 2 − p − q + t ) 4 3 ( 1 − p ) ( 1 − q ) and solving for q gives:
q = 7 p 2 − 2 p − 1 − 4 p 3 + 4 p 2 + p − 1 + ( 4 p 2 − 2 p ) p 2 − p + 1
and substituting u and t into the inradius equations 2 1 ( p + u + 1 ) 4 3 p = 2 1 ( t + u + q ) 4 3 ( 1 − p ) q and solving for q gives:
q = 3 ( 7 p 3 − 9 p 2 + p + 1 ) 8 p 4 − 2 1 p 3 + 1 6 p 2 − 1 1 p + 4 + ( − 8 p 3 − 4 p 2 + 1 2 p − 4 ) p 2 − p + 1
Therefore, q = 7 p 2 − 2 p − 1 − 4 p 3 + 4 p 2 + p − 1 + ( 4 p 2 − 2 p ) p 2 − p + 1 = 3 ( 7 p 3 − 9 p 2 + p + 1 ) 8 p 4 − 2 1 p 3 + 1 6 p 2 − 1 1 p + 4 + ( − 8 p 3 − 4 p 2 + 1 2 p − 4 ) p 2 − p + 1 , which solves to p = 5 1 ( 1 + 2 3 2 − 3 4 ) or p = 8 5 for 0 < p < 1 . However, p = 8 5 leads to q = 1 , so it must be that p = 5 1 ( 1 + 2 3 2 − 3 4 ) .
If p = 5 1 ( 1 + 2 3 2 − 3 4 ) , then u = p 2 − p − 1 = 5 1 ( − 1 + 3 3 2 + 3 4 ) .
The orange circle is an excircle to △ B C D , so the ratio of the radii of the orange and cyan circles is s △ B C D − p s △ B C D = 2 1 ( p + u + 1 ) − p 2 1 ( p + u + 1 ) = 3 2 4 − 1
Therefore, A = 2 , B = 4 , C = 3 , D = 1 , and A B C D = 2 4 .