Voltage Amplifier?
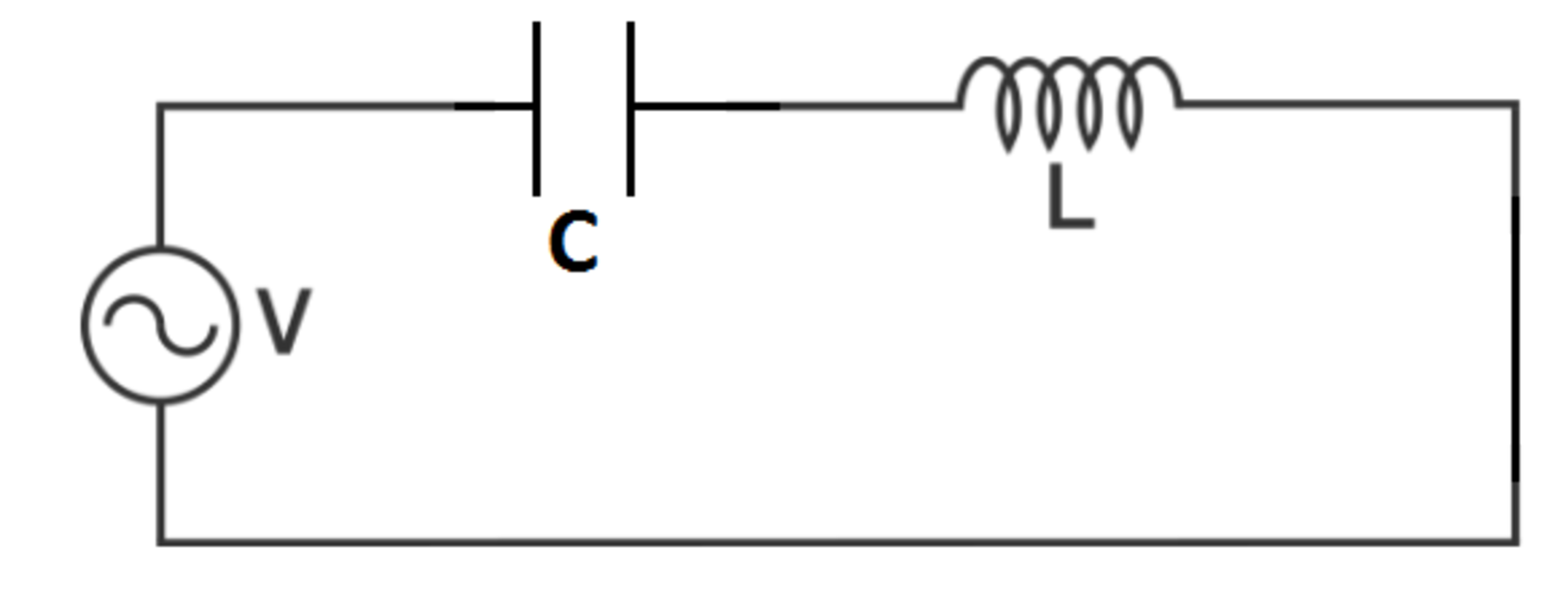
An AC voltage source is connected across a series LC (inductive-capacitive) load. The magnitude of the inductive reactance is twice the magnitude of the capacitive reactance .
In AC steady state, what is the ratio of the amplitude of the voltage across the inductor to the amplitude of the source voltage?
Note: Assume that the source voltage is sinusoidal with a single frequency.
Bonus: What is the phase relationship between these two voltages?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the AC voltage be represented as V ( t ) = V 0 ⋅ s i n ( ω t ) . Given that the inductive impedance is twice that of the capacitive impedance, we have:
∣ j ω L ∣ = 2 ⋅ ∣ j ω C 1 ∣ ⇒ ω L = ω C 2 ⇒ ω 2 L C = 2 .
The voltage across the inductor is determined via a KVL voltage-divider:
V L ( t ) = V ( t ) ⋅ ∣ Z L + Z C ∣ ∣ Z L ∣ = V ( t ) ⋅ ω L − ω C 1 ω L = V ( t ) ⋅ ω 2 L C − 1 ω 2 L C = V ( t ) ⋅ 2 − 1 2 = 2 V ( t ) .
Hence, at AC steady-state: V ( t ) V L ( t ) = V ( t ) 2 ⋅ V ( t ) = 2 : 1 .
Relevant wiki: Impedance
The impedance of the circuit Z = X L − X C
Where, X L and X C are the inductive and the capacitive reactances respectively.
Also, we have, X L = 2 X c
Therefore,
Z = 2 X L
The peak value of current in the circuit will be
i 0 = Z V 0
The peak value of voltage across the inductor will be
V L 0 = i 0 X L = V 0 Z X L = V 0 2
Hence, V 0 V L 0 = 2
Bonus Solution: Let us draw the phasor diagram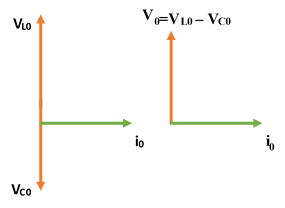 We can see clearly from the phasor diagrams that the voltage across inductor and the source voltage are in the same phase.
We can see clearly from the phasor diagrams that the voltage across inductor and the source voltage are in the same phase.