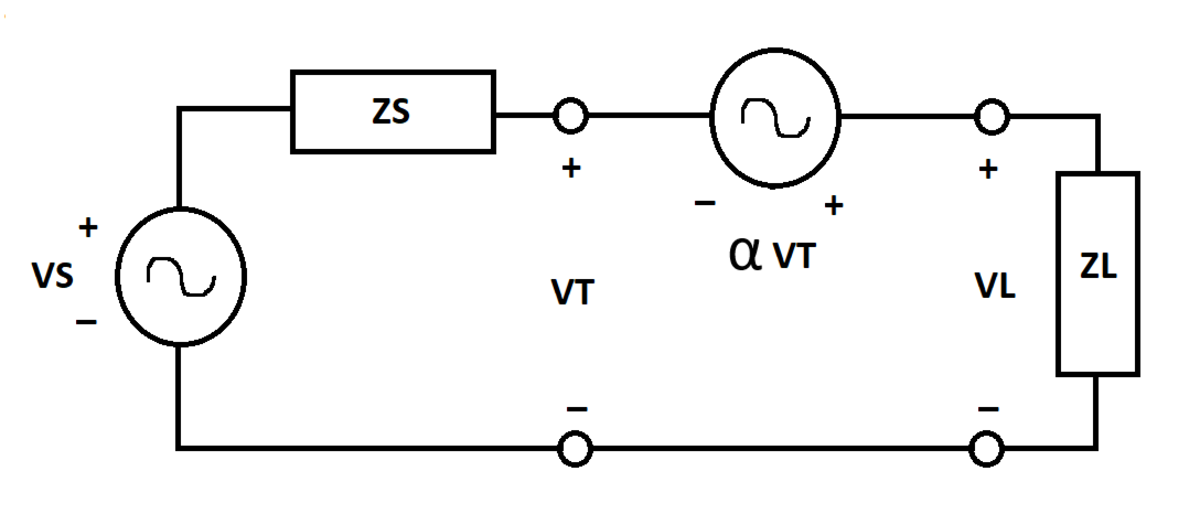
Voltage-Controlled Voltage Source

There are several ways to present the solution. My preference is to invoke continuity of current in the circuit (since everything is in series).

$\frac{V_S - V_T}{Z_S} = \frac{V_T + \alpha V_T}{Z_L}$

Solve that equation for $V_T$ , and then $V_L = V_T + \alpha V_T$

The negative terminal of the source $S$ is considered to be at $0 \ \mathrm{V}$ . Keeping this in mind, the circuit equations are:

$-V_S + IZ_S - \alpha V_T + IZ_L=0$ $V_S - V_T=IZ_S$ $IZ_L = V_L$

Writing these equations in a matrix form leads to:

$\left[ \begin{matrix} Z_S+Z_L&-\alpha\\Z_S&1\end{matrix} \right]\left[ \begin{matrix} I\\V_T \end{matrix} \right]=\left[ \begin{matrix} V_S\\V_S \end{matrix} \right]$ $\implies V_L = \left[ \begin{matrix} Z_L & 0 \end{matrix} \right]\left[ \begin{matrix} I\\V_T \end{matrix} \right] = \left[ \begin{matrix} Z_L & 0 \end{matrix} \right] \left[ \begin{matrix} Z_S+Z_L&-\alpha\\Z_S&1\end{matrix} \right]^{-1} \left[ \begin{matrix} V_S\\V_S \end{matrix} \right]$

Finally:

$\lvert V_L \rvert = \Biggr\lvert \left[ \begin{matrix} Z_L & 0 \end{matrix} \right] \left[ \begin{matrix} Z_S+Z_L&-\alpha\\Z_S&1\end{matrix} \right]^{-1} \left[ \begin{matrix} V_S\\V_S \end{matrix} \right] \Biggr\rvert \approx 11.335$