Voltage divider

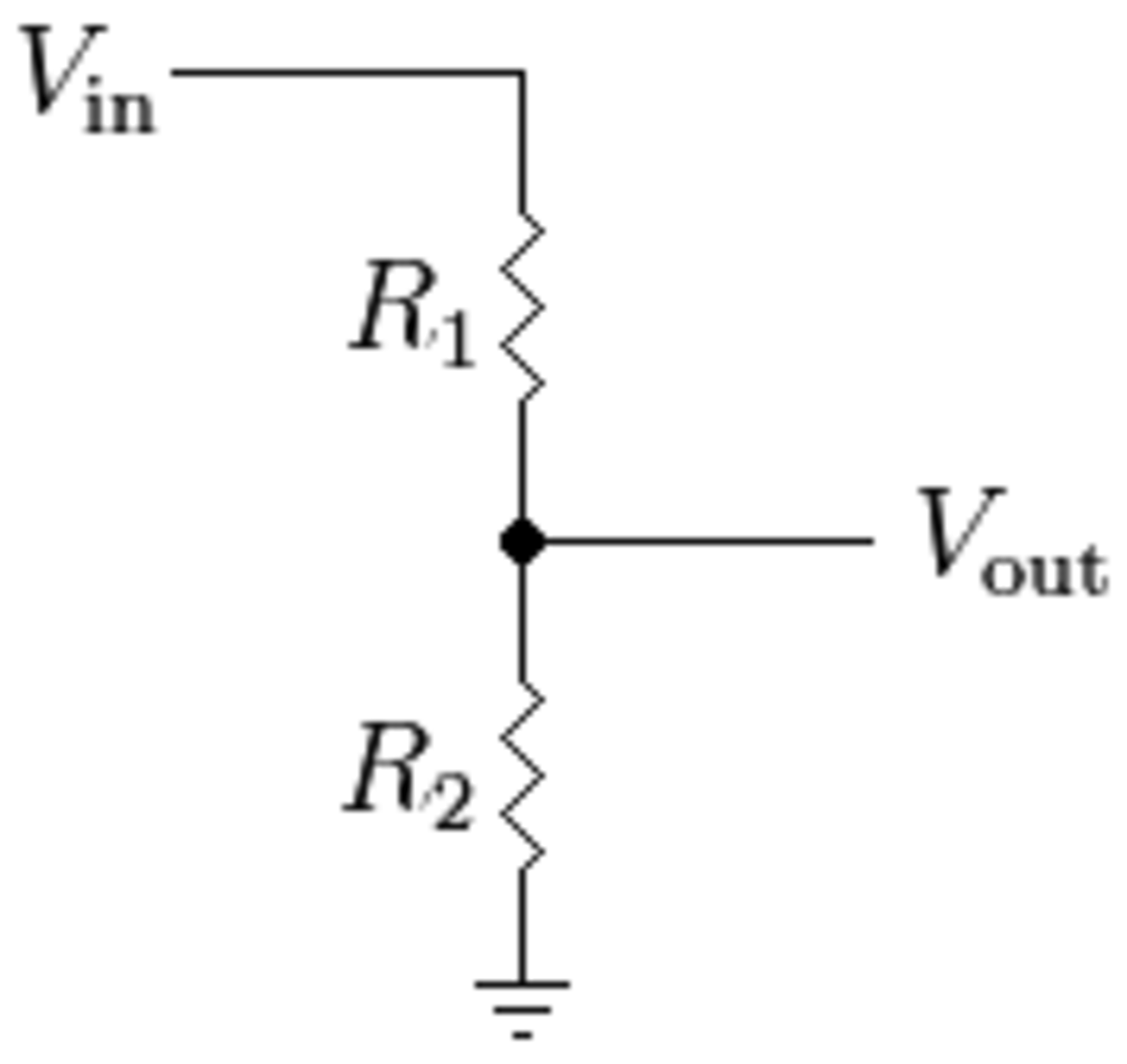
Electricity and Magnetism Level pending

Often a device cannot sustain higher voltage than a certain threshold, because it's at risk of burning out due to high thermal power releases, which are proportional to voltage. The input voltage can be adjusted using a voltage divider as shown in the circuit below: the input voltage $V_{in}$ drops after passing through $R_1$ , and we can extract a lower voltage $V_{out}$ . The end of the circuit is grounded (reference point, zero potential). What should be the ratio of $R_1$ to $R_2$ so that the ratio of voltages is $V_{in}/V_{out} = 3$ ?

The answer is 2.

7 solutions

Discussions for this problem are now closed

Jordan Osborn
Aug 6, 2013

The formula for voltage dividers is $\frac {V_{in}} {V_{out}} = \frac {R_1 + R_2} {R_2}$ If we rearrange this formula we get $\frac {V_{in}} {V_{out}} = \frac {R_1} {R_2} + \frac {R_2} {R_2}$ Which can be simplified to $\frac {V_{in}} {V_{out}} = \frac {R_1} {R_2} + 1$ As $\frac {V_{in}} {V_{out}} = 3$ We can now solve $3 = 1 + \frac {R_1} {R_2}$ $\frac {R_1} {R_2} = 2$ The ratio of the resistors resistance is therefore 2

the best one........

Kushaagra Goyal - 7 years, 10 months ago

Not the best one, the way I look at it; it depends on memorizing a formula. I think it is better to understand what is happening in the circuit.

In this case, the source voltage is what pushes the current through the resistors. If V-out were halfway along the circuit then the voltage there would be half, and so on - because half of all the pushing power was used on the first half of the circuit. If V-out were 9/10 of the way around the circuit then only 1/10 of the pushing power is left there.

By 'halfway along' we are measuring in Ohms, not in meters :)

Matt McNabb - 7 years, 10 months ago

Memorising a formula and understanding what is going on in the circuit are not mutually exclusive.

Jordan Osborn - 7 years, 10 months ago

Haroun Meghaichi
Aug 10, 2013

Note That $V_{\text{in}}=(R_1+R_2)I$ , and $V_{\text{out}}=R_2 I$ .

From the first equation : $I=\frac{V_{\text{in}}}{R_1+R_2}$ , which means that : $V_{\text{out}}=\frac{R_2 V_{\text{in}}}{R_1+R_2}.$ from the ratio condition ,this is equivalent to : $3R_2=R_2+R_1$ ,

which means that ; $\frac{R_1}{R_2}=2.$

Caroline Rui
Aug 8, 2013

i=Vin/(R1+R2) : (R2/R2) = (Vin/R2)/(R1/R2+1)

Vout=i.R2= (Vin/R2)/(R1/R2+1).R2

Vout=(Vin)/(R1/R2+1)

Vin/Vout=(R1/R2+1) 3=R1/R2+1

R1/R2=2

Ivan Sekovanić
Aug 6, 2013

Note that according to Ohm's law, $I=\frac{V}{R}$ . Now, taking into account that this is a series circuit, we may note $2$ things:

The total resistance $R_{total}=R_{1}+R_{2}$ .
The current is even in any segment of the circuit, meaning that according to Ohm's Law $\frac{V_{in}}{R_{total}}=\frac{V_{out}}{R_{2}}$ .

With the above statements in mind, it is obvious that

$\frac{V_{in}}{R_{1}+R_{2}}=\frac{V_{out}}{R_{2}}\Rightarrow \frac{V_{in}}{V_{out}}=\frac{R_{1}+R_{2}}{R_{2}} \Rightarrow \frac{R_{1}+R_{2}}{R_{2}}=3 \Rightarrow \frac{R_{1}}{R_{2}}+\frac{R_{2}}{R_{2}}=3 \Rightarrow$

$\Rightarrow \frac{R_{1}}{R_{2}}+1=3 \Rightarrow \frac{R_{1}}{R_{2}}=2$ , which is the ratio we are looking for.

Why is the current even in every segment of the circuit??

Krishna Jha - 7 years, 10 months ago

The current (coulombs per second) is the rate that electrons are moving through the wire. You can treat the electrons as a rigid series, like a bicycle chain - they can't bunch up or spread out.

If the electrons move at a certain rate through one part of the wire and there's no junctions they must be moving at the same rate everywhere.

When they get to the "V-out point", if any current is actually drawn there, then the current will split. However this doesn't affect the voltage at V-out if current is drawn (that voltage is solely determined by the source voltage and the strength of R1). So these calculations are assuming we measure V-out without drawing off any current there.

Matt McNabb - 7 years, 10 months ago

I have to say, I really love your explanations. They cover everything required and are easily understandable. Thank you very much, Matt :)

Ivan Sekovanić - 7 years, 10 months ago

This is, I believe, due to the fact that in a series circuit, the current goes through all of the components in the circuit and can flow in only one direction. Thus, all the segments have the same current.

If you have a better explanation please enlighten me, I would like to know. :)

PS: Also, feel free to let me know if I expressed myself in a wrong way. I am not that experienced when it comes to Physics.

Ivan Sekovanić - 7 years, 10 months ago

Divyansh Singhal
Aug 6, 2013

{V(in)-V(out)}/i=R(1) .....(1) AND, {V(out)-0}/i=R(2) ......(2) Hence on dividing (1)by (2) we get the ratio to be equal to {V(in)-V(out)}/V(out) also we are given that V(in)=3V(out), So, the ratio obtained is equal to 2.

Lawrence Limesa
Aug 5, 2013

Generally, The formula is $V_{out} = \frac{R_2}{R_2+R_1} \times V_{in}$

$\frac{V_{out}}{V_{in}} = \frac{R_2}{R_2+R_1}$ , subtituting $\frac{V_{out}}{V_{in}}=\frac{1}{3}$ we get that, $2 \times R_2 = R_1$ so the ratio of $R_1$ to $R_2$ is $2$

Maharnab Mitra
Aug 5, 2013

Let $V_{in}$ be 3k and $V_{out}$ be k. Let the current be i.

Therefore, potential drop across $R_{1}$ =i $R_{1}$ =2k......................(1)

Potential drop across $R_{2}$ =i $R_{2}$ =k......................(2)

Dividing (1) and (2), we get $R_{1}$ / $R_{2}$ = 2

Voltage divider

The answer is 2.

7 solutions

Discussions for this problem are now closed

0 pending reports