Voltage Equalization

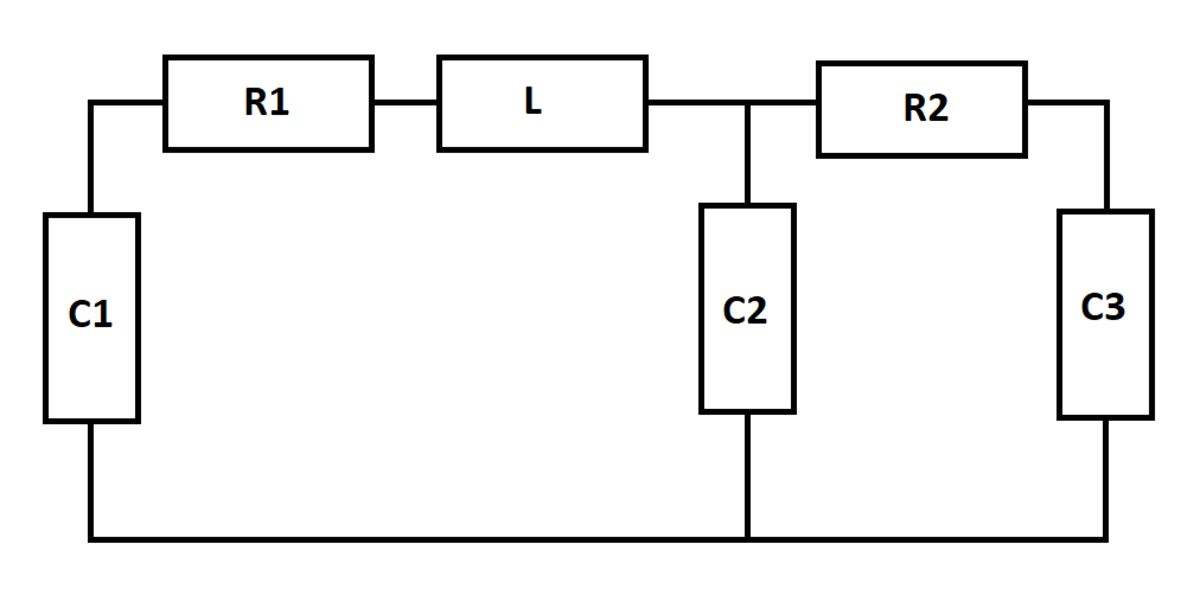
Electricity and Magnetism Level pending

In the $RLC$ network shown below, capacitor $C_1$ has a voltage of $10$ at time $t = 0$ . The other capacitors and the inductor are de-energized at that time. Let $V_{C1 min}$ be the smallest value of the voltage across capacitor $C_1$ over all time. Let $V_{C2 max}$ be the largest value of the voltage across capacitor $C_2$ over all time. Let $V_\infty$ be the limiting value of all three capacitor voltages as the elapsed time approaches infinity.

Determine the following ratio:

$\large{\frac{V_{C1 min} + V_{C2 max} }{V_\infty}}$

Details and Assumptions
1) $R_1 = 1$
2) $R_2 = 2$
3) $C_1 = 1$
4) $C_2 = 2$
5) $C_3 = 3$
6) $L = 1$
7) All three voltage values in the ratio are positive numbers

The answer is 2.693.

1 solution

Steven Chase
Feb 23, 2020

The state variables are $(V_{C1}, V_{C2}, V_{C3}, I_L)$ . Fundamental equations:

$I_{C1} = C_1 \dot{V}_{C1} \\ I_{C2} = C_2 \dot{V}_{C2} \\ I_{C3} = C_3 \dot{V}_{C3} \\ V_L = L \dot{I}_L$

Writing the left sides in terms of the state variables results in:

$-I_L = C_1 \dot{V}_{C1} \\ I_L - \frac{V_{C2} - V_{C3}}{R_2} = C_2 \dot{V}_{C2} \\ \frac{V_{C2} - V_{C3}}{R_2} = C_3 \dot{V}_{C3} \\ V_{C1} - R_1 I_L - V_{C2} = L \dot{I}_L$

Numerical integration results in the following voltage plots. All three capacitor voltages converge over time, as expected:

Voltage Equalization

The answer is 2.693.

1 solution

0 pending reports