Voltage Transfer Function (Part 1)
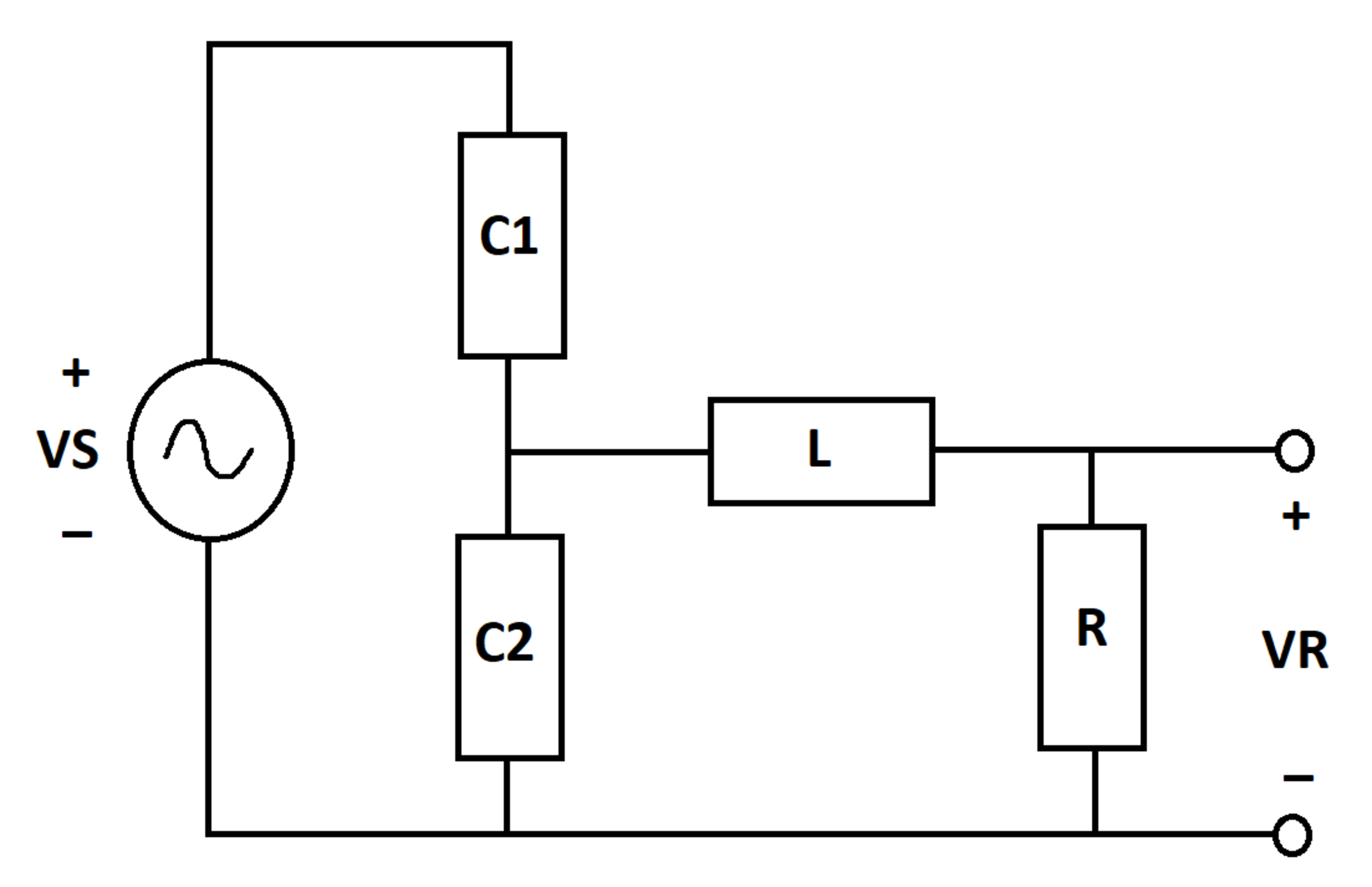
A sinusoidal voltage source excites an electrical network as shown. The voltage across the resistor is . In steady-state, the relationship between the two voltages is:
In the above equation, is a scalar "gain" parameter, and (in radians) is the phase angle of the resistor voltage with respect to the source voltage.
Enter your answer as the product of and
Details and Assumptions:
1)
Source angular frequency
2)
3)
4)
The quantity
is the imaginary unit
5)
and
are expressed as complex numbers
The answer is -0.16308.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the input voltage be V S = sin ( ω t ) . Since the source frequency is ω , inductive, resistive and capacitive reactances are:
Z L = j L ω Z R = R Z C 1 = ω C 1 − j Z C 2 = ω C 2 − j
In steady-state, the source voltage magnitude is defined, for convenience, as V S = 1 + j 0
Now, let the steady stare source current be I , that through the inductive branch be I 1 and through the capacitive branch be I 2 . Then, according to Kirchoff's laws:
− V S + Z C 1 I + Z C 2 I 2 = 0 ( R + Z L ) I 1 = Z C 2 I 2 I = I 1 + I 2
Solving for I 1 gives:
I 1 = Z C 1 + ( 1 + Z C 2 Z C 1 ) ( R + Z L ) V S V R = Z C 1 + ( 1 + Z C 2 Z C 1 ) ( R + Z L ) V S R
The above quantity V R is a complex number. According to the problem statement, this leads to the conclusion that:
α e j θ = Z C 1 + ( 1 + Z C 2 Z C 1 ) ( R + Z L ) R
Substituting all values and ω = 1 , and computing V R leads to the following complex number:
α e j θ = 0 . 2 3 0 8 − j 0 . 1 5 3 8
This complex number has an argument:
θ = − arctan ( 0 . 2 3 0 8 0 . 1 5 3 8 ) α = 0 . 2 3 0 8 2 + 0 . 1 5 3 8 2
The answer turns out to be α θ ≈ − 0 . 1 6 3 1