Volume
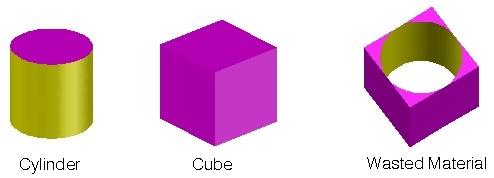 If the largest right circular cylinder is cut from a cube with side
a
, what is the ratio of the volume of the wasted material to the volume of the cylinder?
If the largest right circular cylinder is cut from a cube with side
a
, what is the ratio of the volume of the wasted material to the volume of the cylinder?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
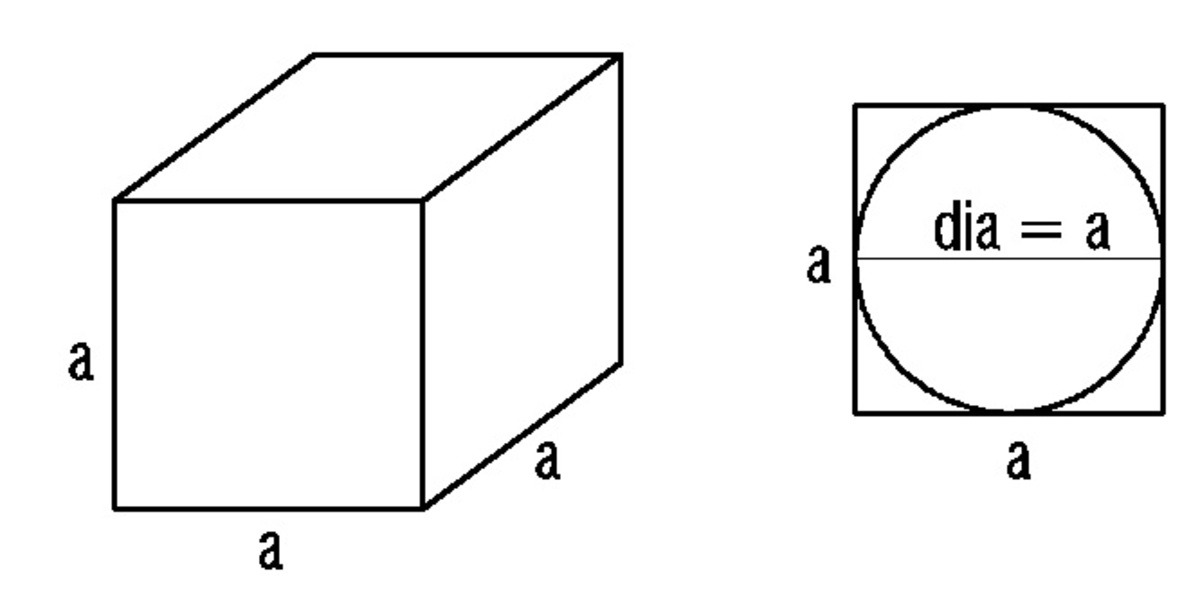 Solving for the volume of the cube
Solving for the volume of the cube
V c u b e = a 3
Solving for the volume of the cylinder
V c y l i n d e r = A b a s e h = 4 π ( a 2 ) ( a ) = 4 π a 3
Solving for the volume of the wasted material
V w a s t e d − m a t e r i a l = V c u b e − V c y l i n d e r = a 3 − 4 π a 3 = a 3 ( 1 − 4 π )
Solving for the ratio
V c y l i n d e r V w a s t e d − m a t e r i a l = 4 π ( a 3 ) a 3 ( 1 − 4 π ) = π 4 − 1
This is really a two dimensional problem, as the same height multiplies everything. So all we need to deal with is a square and a circle.
We can arbitrarily set the radius of the circle as 1 (since we are only interested in ratios of sizes not the actual values). Area A c i r c l e = π .
Side of the square will be the diameter, 2, giving us the area A s q u a r e = 4 .
So the ratio will be π 4 − π = π 4 − 1