Volume bounded by two hyperboloids
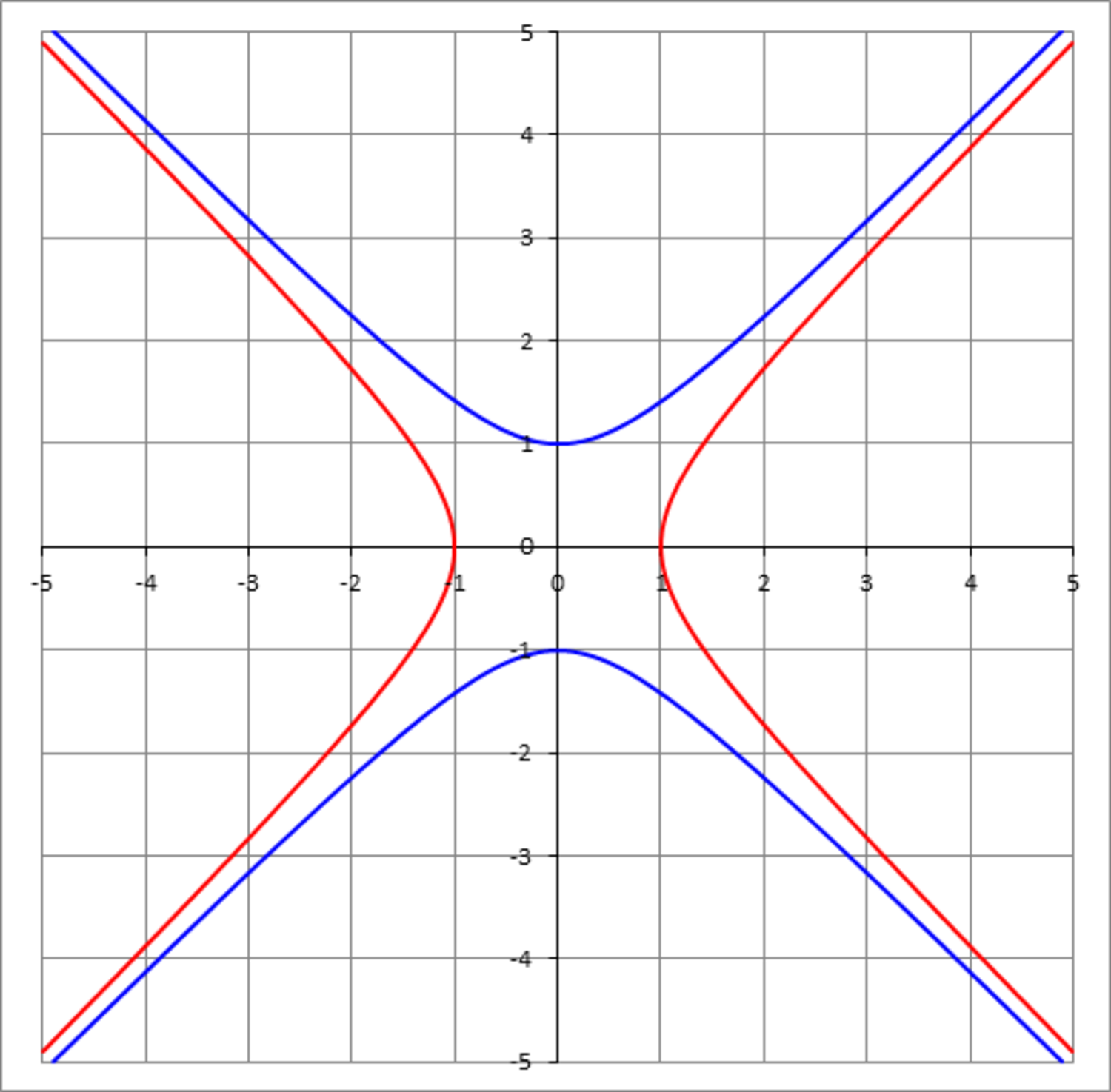
The figure above shows a cross section (at y = 0 ) through the hyperboloid of one sheet (red) given by
x 2 + y 2 − z 2 = 1
and the hyperboloid of two sheets (blue) given by
x 2 + y 2 − z 2 = − 1
Find the volume bounded by the two hyperboloids and z = − 5 and z = 5 . The volume can be written as b a π for positive coprime integers a , b . Find a + b .
The answer is 59.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Comparing the volumes of revolution, we want to calculate π ∫ − 5 5 ( z 2 + 1 ) d z − 2 π ∫ 1 5 ( z 2 − 1 ) d z = 3 5 6 π making the answer 5 6 + 3 = 5 9 .
If we look at the boundaries for the outer function for positive z (due to symmetry, we can multiply by 2 to get the total volume), we get
0 ≤ r ≤ z 2 + 1 0 ≤ θ ≤ 2 π 0 ≤ z ≤ 5
And for the inner function, we get
0 ≤ r ≤ z 2 − 1 0 ≤ θ ≤ 2 π 1 ≤ z ≤ 5
Then we get this expression for the total volume:
2 [ ∫ 0 5 ∫ 0 2 π ∫ 0 z 2 + 1 r d r d θ d z − ∫ 1 5 ∫ 0 2 π ∫ 0 z 2 − 1 r d r d θ d z ]
= ∫ 0 5 ∫ 0 2 π z 2 + 1 d θ d z − ∫ 1 5 ∫ 0 2 π z 2 − 1 d θ d z = ∫ 0 5 ∫ 0 2 π z 2 + 1 d θ d z − ∫ 1 5 ∫ 0 2 π z 2 − 1 d θ d z
= ∫ 0 5 ( 2 π ) ( z 2 + 1 ) d z − ∫ 1 5 ( 2 π ) ( z 2 − 1 ) d z
= ( 2 π ) ( 3 z 3 + 1 + z ) ∣ ∣ ∣ 0 5 − ( 2 π ) ( 3 z 3 + 1 − z ) ∣ ∣ ∣ 1 5
= 3 5 6 π
a + b = 5 6 + 3 = 5 9