Volume Calculation for an Icosidodecahedron
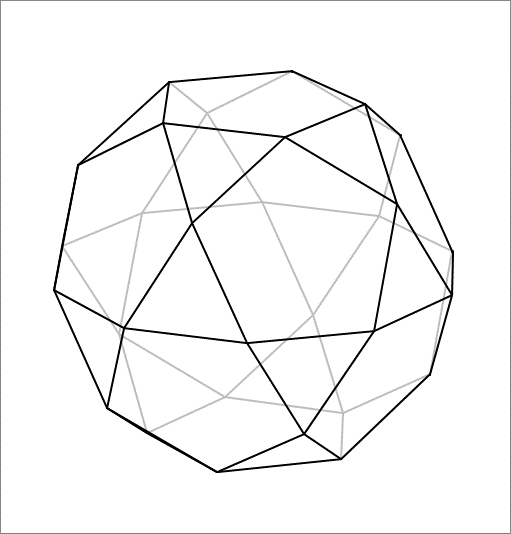
The so-called icosidodecahedron is depicted in the figure above. It is the solid that results from the intersection of a dodecahedron and an icosahedron of a specific relative scale. Its faces comprise 1 2 regular pentagons and 2 0 equilateral triangles, all of the same edge length. If the edge length is 1 then find the volume of the polyhedron.
The answer is 13.8355.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
For a regular n-gon with side 1, the distance from centre to a vertex is given by r n = 2 sin π / n 1 and its area is given by A n = 4 tan π / n n
If you look carefully you can see that between opposite pentagons there is a regular 10-gon dividing the solid in half. This means that the distance from the centre to any vertex equals r 1 0 and the distance from the centre to each of the faces can be calculated using pythagoras: h n = r 1 0 2 − r n 2
The volume of the pyramid that a face has to the centre is given by V n = 3 1 A n h n
Now the total volume is the sum of 32 such pyramids:
1
2
V
5
+
2
0
V
3
≈
1
3
.
8
3
5
5
2
5
9
4

I used the shortcut of looking up the formula of icosahedron, and from the question deduced that the original one before the trimming is size 2. Then I just deducted the volume of 12 pentamids from the results.
Formula for volume of icosahedron.
= 5(3 + √5)s³ / 12.
V_icos(2) = (30 + 10√5) / 3.
Volume of a unit of icosahedral vertices' uniform pentamid of size 1.
= (5 + √5) / 24.
Volume of icosidodecahedron.
= V_icos(2) - 12 x [(5 + √5) / 24].
= (45 + 17√5) /6
If you extend the faces of all the pentagons of the icosidodecahedron, it will form a dodecahedron where each vertex is centered above one of the equilateral triangles.
A pentagon in the icosidodecahedron can be formed by joining the midpoints of a pentagon in the dodecahedron. Since the icosidodecahedron pentagon has sides of 1 , the dodecahedron pentagon has sides of s = 2 ⋅ 2 1 sec 3 6 ° = 2 1 ( 5 − 1 ) . That makes the volume of the dodecahedron:
V dodec = 4 1 ( 1 5 + 7 5 ) s 3 = 4 1 ( 1 5 + 7 5 ) ( 2 1 ( 5 − 1 ) ) 3 = 1 0 + 2 5
Each of the "extra" 2 0 pyramids formed by the difference of the dodecahedron and icosidodecahedron have equilateral triangle bases with sides of 1 and lateral edges of l = 2 1 s = 4 1 ( 5 − 1 ) . The radius of the equilateral triangle base is r = 3 1 , so by the Pythagorean Theorem the height of the pyramid is h = l 2 − r 2 = ( 4 1 ( 5 − 1 ) ) 2 − ( 3 1 ) 2 = 6 1 ( 3 3 − 1 5 ) . That makes the volume of each pyramid:
V pyr = 3 1 ⋅ 4 3 ⋅ 1 2 ⋅ 6 1 ( 3 3 − 1 5 ) = 2 4 1 ( 3 − 5 )
Since the volume of the icosidodecahedron is the volume of a dodecahedron minus the volume of 2 0 pyramids with equilateral triangle bases:
V ico = V dodec − 2 0 ⋅ V pyr = 1 0 + 2 5 − 2 0 ⋅ 2 4 1 ( 3 − 5 ) = 6 1 ( 4 5 + 1 7 5 ) ≈ 1 3 . 8 3 5 5