Volume Festival.
Let ( ∣ x ∣ < 1 ) and f ( x ) = n = 0 ∑ ∞ ( ( 2 2 n + 1 ) ! ( 2 − 2 n − 3 ) ! ∗ ( a + n d ) x n ) and g ( x ) = n = 0 ∑ ∞ ( a ∗ + n 2 d ∗ ) x n .
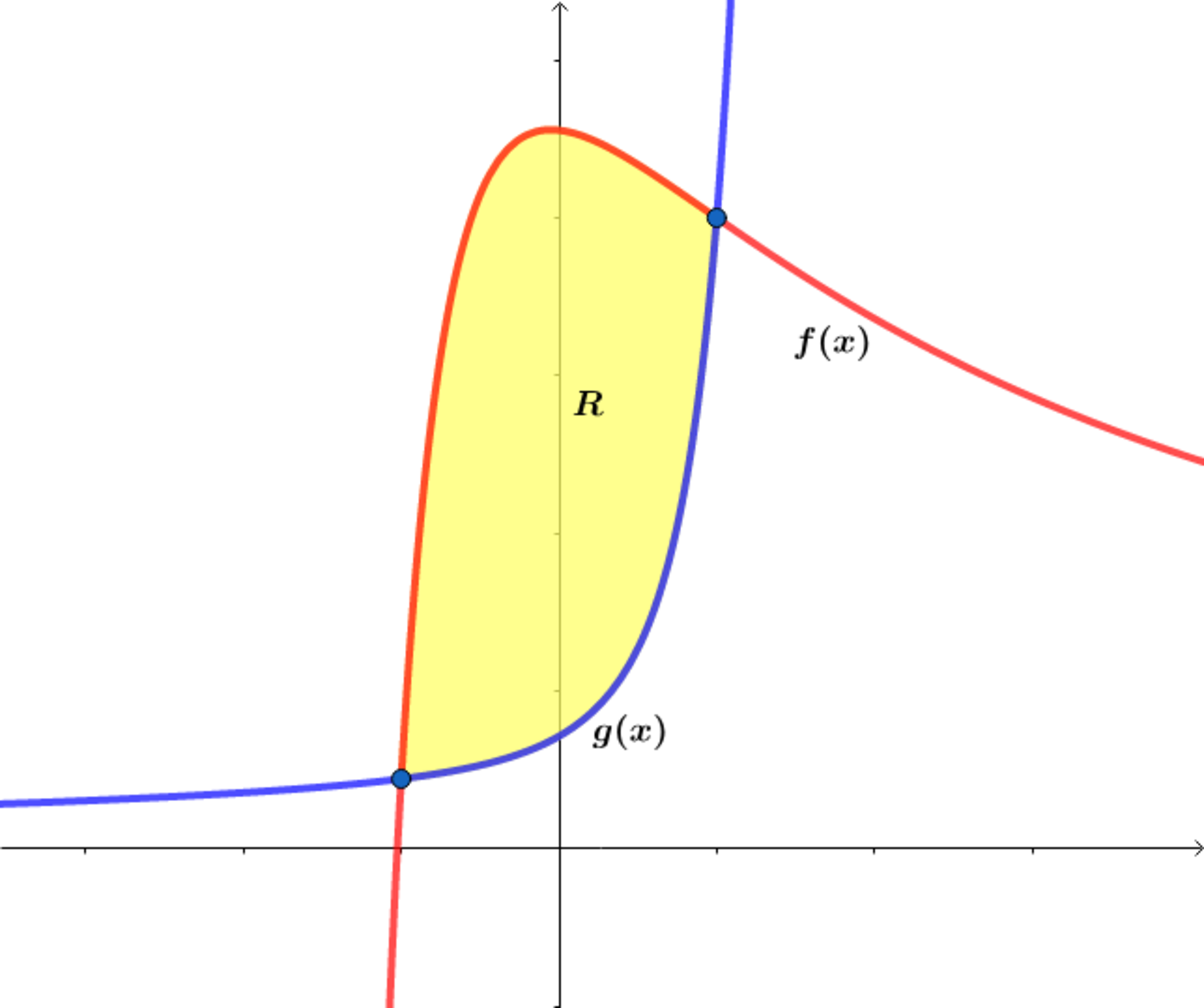
If f ( 2 1 ) = g ( 2 1 ) = 2 and f ( − 2 1 ) = g ( − 2 1 ) = 9 2 and the volume V of the region bounded by f ( x ) and g ( x ) on [ − 2 1 , 2 1 ] when revolved about the x axis can be expressed as V = β α π , where gcf ( α , β ) = 1 , find α + β .
The answer is 841517.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the gamma function Γ ( p ) = ∫ 0 ∞ t p − 1 e − t d t we obtain:
Γ ( 2 1 ) = ∫ 0 ∞ t − 2 1 e − t d t
Let s 2 = t ⟹ 2 s d s = d t ⟹
Γ ( 2 1 ) = 2 ∫ 0 ∞ e − s 2 d s
Since s is a dummy variable we can write:
( Γ ( 2 1 ) ) 2 = 4 ∫ 0 ∞ e − x 2 d x ∫ 0 ∞ e − y 2 d y = 4 ∫ 0 ∞ ∫ 0 ∞ e − ( x 2 + y 2 ) d x d y
Let x = r cos θ , y = r sin θ
Using the Jacobian ⟹ ( Γ ( 2 1 ) ) 2 = 4 ∫ 0 2 π ∫ 0 ∞ e − r 2 r d r d θ = − 2 ∫ 0 2 π e − r 2 ∣ 0 ∞ d θ = 2 ∫ 0 2 π d θ = π ⟹ Γ ( 2 1 ) = π
Now, using integration by parts you can show that Γ ( p + 1 ) = p Γ ( p )
Show Γ ( 1 ) = 1 and recursively using Γ ( p + 1 ) = p Γ ( p ) ⟹ Γ ( p + 1 ) = p ! for any integer p ≥ 0 and p can be extended to reals so that Γ ( 2 1 ) = Γ ( 2 − 1 + 1 ) = π = ( 2 − 1 ) !
Using Γ ( p + 1 ) = p Γ ( p ) and Γ ( 2 1 ) = π = ( 2 − 1 ) !
⟹
S 0 = Γ ( 2 3 ) = 2 1 ∗ Γ ( 2 1 ) = 2 π = ( 2 1 ) !
S 1 = Γ ( 2 5 ) = 2 3 ∗ Γ ( 2 3 ) = 2 2 1 ∗ 3 ∗ π = ( 2 3 ) !
S 2 = Γ ( 2 7 ) = 2 5 ∗ Γ ( 2 5 ) = 2 3 1 ∗ 3 ∗ 5 ∗ π = ( 2 5 ) !
In General:
S n = Γ ( 2 2 n + 3 ) = 2 n + 1 1 ∗ 3 ∗ 5 ∗ ∗ ∗ ( 2 n + 1 ) ∗ π = ( n + 2 1 ) !
⟹ ( n + 2 1 ) ! = 2 2 n + 1 ∗ n ! ( 2 n + 1 ) ! ∗ π , where n is a non-negative integer.
Note: ( 2 n + 1 ) ! = 1 ∗ 2 ∗ 3 ∗ ∗ ∗ ( 2 n ) ∗ ( 2 n + 1 ) = 2 n ∗ n ! ∗ ( 1 ∗ 3 ∗ 5 ∗ ∗ ∗ ( 2 n + 1 ) ) ⟹ 1 ∗ 3 ∗ 5 ∗ ∗ ∗ ( 2 n + 1 ) = 2 n ∗ n ! ( 2 n + 1 ) !
and,
Using Γ ( p ) = p Γ ( p + 1 ) and Γ ( 2 1 ) = π = ( 2 − 1 ) !
⟹
T 0 = Γ ( − 2 1 ) = − 2 Γ ( 2 1 ) = − 2 π = ( − 2 3 ) !
T 1 = Γ ( − 2 3 ) = − 3 2 Γ ( − 2 1 ) = 1 ∗ 3 2 2 π = ( − 2 5 ) !
T 2 = Γ ( − 2 5 ) = − 5 2 Γ ( − 2 3 ) = − 1 ∗ 3 ∗ 5 2 3 π = ( − 2 7 ) !
In General:
T n = Γ ( − n − 2 1 ) = ± 1 ∗ 3 ∗ 5 ∗ ∗ ∗ ( 2 n + 1 ) 2 n + 1 π = ( − n − 2 3 ) !
⟹ ( − n − 2 3 ) ! = ± ( 2 n + 1 ) ! 2 2 n + 1 ∗ n ! π , where n is a non-negative integer
⟹
S n ∗ T n = { π − π for n odd for n even .
Let ∣ x ∣ < 1 .
n = 0 ∑ ∞ ( a + n d ) x n = a n = 0 ∑ ∞ x n + d n = 1 ∑ ∞ n x n = 1 − x a + d j = 1 ∑ ∞ n = j ∑ ∞ x n = 1 − x a + 1 − x d j = 1 ∑ ∞ x j = 1 − x a + 1 − x d ( 1 − x x ) = 1 − x a + ( 1 − x ) 2 d x
⟹
f ( x ) = n = 0 ∑ ∞ ( ( 2 2 n + 1 ) ! ( 2 − 2 n − 3 ) ! ∗ ( a + n d ) x n ) = − π n = 0 ∑ ∞ ( − 1 ) n ( a + n d ) x n = − π ( 1 + x a − ( 1 + x ) 2 d x )
and,
g ( x ) = n = 0 ∑ ∞ ( a ∗ + n 2 d ∗ ) x n = a ∗ n = 0 ∑ ∞ x n + d ∗ n = 1 ∑ ∞ n 2 x n = 1 − x a ∗ + d ∗ j = 1 ∑ ∞ n = j ∑ ∞ n x n = ( 1 − x a ∗ + d ∗ j = 1 ∑ ∞ ( j x j + ( j + 1 ) x j + 1 + ( j + 2 ) x j + 2 + . . . ) = 1 − x a ∗ + d ∗ ( 1 − x 1 j = 1 ∑ ∞ j x j + ( 1 − x ) 2 x j = 1 ∑ ∞ x j ) = 1 − x a ∗ + d ∗ ( ( 1 − x 1 ) ( ( 1 − x ) 2 x ) + ( ( 1 − x ) 2 x ) ( 1 − x x ) ) = 1 − x a ∗ + d ∗ ( ( 1 − x ) 3 x 2 + x )
f ( 2 1 ) = 2 and f ( − 2 1 ) = 9 2 ⟹
3 a − d = π − 9
a + d = 9 π − 1
⟹ a = 1 8 π − 4 1 and d = 6 π 1 3 ⟹ f ( x ) = 6 1 ( 3 ( 1 + x ) 4 1 + ( 1 + x ) 2 1 3 x ) = 1 8 1 ( ( 1 + x ) 2 8 0 x + 4 1 )
Let u = 1 + x ⟹ d x = d u ⟹ ∫ − 2 1 2 1 ( f ( x ) ) 2 d x = 1 8 2 1 ∫ 2 1 2 3 u 4 ( 8 0 u − 3 9 ) 2 d u = 1 8 2 1 ∫ 2 1 2 3 6 4 0 0 u − 2 − 6 2 4 0 u − 3 + 1 5 2 1 u − 4 d u = 1 8 2 1 ( − u 6 4 0 0 + u 2 3 1 2 0 − u 3 5 0 7 ) ∣ 2 1 2 3 = 7 2 9 3 0 2 8 .
g ( 2 1 ) = 2 and g ( − 2 1 ) = 9 2 ⟹
9 a ∗ − d ∗ = 3
a ∗ + 3 d ∗ = 1
⟹ a ∗ = 1 4 5 and d ∗ = 1 4 3 ⟹ g ( x ) = 1 4 1 ( 1 − x 5 + ( 1 − x ) 3 3 ( x 2 + x ) )
∫ − 2 1 2 1 ( g ( x ) ) 2 d x = 1 4 2 1 ∫ − 2 1 2 1 ( 1 − x ) 2 2 5 + ( 1 − x ) 4 3 0 x ( x + 1 ) + ( 1 − x ) 6 9 x 2 ( x + 1 ) 2 d x
Let I 1 ( x ) = ∫ ( 1 − x ) 4 x ( x + 1 ) d x
Letting u = 1 − x ⟹ d x − − d u ⟹ I 1 ( x ) = − ∫ u − 2 − 3 u − 3 + 2 u − 4 d u = 1 − x 1 − 2 ( 1 − x ) 2 3 + 3 ( 1 − x ) 3 2
⟹ I 1 ( x ) ∣ − 2 1 2 1 = 8 1 9 2
Let I 2 ( x ) = ∫ ( 1 − x ) 6 x 2 ( x + 1 ) 2 d x
Letting u = 1 − x ⟹ d x − − d u ⟹ I 2 = − ∫ u − 2 − 6 u − 3 + 1 3 u − 4 − 1 2 u − 5 + 4 u − 6 d u = 1 − x 1 − ( 1 − x ) 2 3 + 3 ( 1 − x ) 3 1 3 − ( 1 − x ) 4 3 + 5 ( 1 − x ) 5 4
⟹ I 2 ( x ) ∣ − 2 1 2 1 = 1 2 1 5 2 5 9 6
and,
I 3 = ∫ − 2 1 2 1 ( 1 − x ) − 2 d x = 1 − x 1 ∣ − 2 1 2 1 = 3 4
⟹ ∫ − 2 1 2 1 ( g ( x ) ) 2 = 1 4 2 1 ( 3 1 0 0 + 8 1 2 7 6 0 + 1 2 1 5 2 3 3 6 4 ) = 6 6 1 5 2 9 2 4
⟹ V = π ∫ − 2 1 2 1 ( f ( x ) ) 2 − ( g ( x ) ) 2 d x = 1 7 8 6 0 5 6 6 2 9 1 2 π = β α π ⟹ α + β = 8 4 1 5 1 7 .