Volume flow rate of a piston

Classical Mechanics Level 2

An engine's piston moves at an average speed of 10 m/s \text{m/s} while pulling the air-fuel mixture through a 3 cm \text{cm} by 2 cm \text{cm} rectangular intake valve. Find the average volume flow rate for the air-fuel mixture entering the piston in m 3 s \frac{\text{m}^3}{s} . (Assume the piston has the same cross-sectional dimensions as the intake valve.)

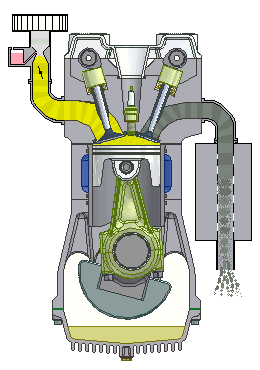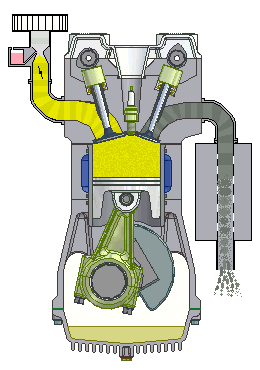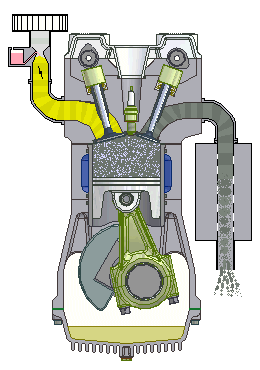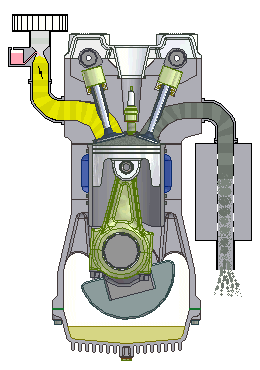This four-stroke engine goes through the stages of intake, compression, combustion, and exhaust. This four-stroke engine goes through the stages of intake, compression, combustion, and exhaust.


The answer is 0.006.

July Thomas by July Thomas , 30, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

July Thomas
Apr 13, 2016

Relevant wiki: Continuity Equation (Fluids)

volume flow rate = A v = [ ( 0.02 m ) ( 0.03 m ) ] ( 10 m/s ) = 6 × 1 0 − 3 m 3 s = 6 m 3 s \text{volume flow rate} = Av = [(0.02 \text{m})(0.03 \text{m})](10 \text{m/s}) = 6 \times 10^{-3} \frac{\text{m}^3}{\text{s}} = 6 \frac{\text{m}^3}{\text{s}}

4 Helpful 0 Interesting 0 Brilliant 0 Confused

And how do you know the density? You can't just convert volume into mass!!!

Mujibur Bhuniyan - 5 years ago

Log in to reply

Hey Mujibur, there was a conflict between the units asked for in my problem and the units of volume flow rate. I edited the problem and my solution. I hope this fixes it!

July Thomas - 4 years, 12 months ago

This is continuity Equation the Density is constant so therefor there is no need to find for density in this equation. If you want density use gas law friend.

Gabriel Enrique Marcial - 3 years, 9 months ago

how can 6E-3 be equal to 6 ?

Paul MEYNCKENS - 2 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...