Volume intersection of two cubes
Find the volume of intersection of two unit cubes with a common main diagonal. One cube is rotated by 6 0 ∘ about common diagonal. The volume equals to B A , where A and B are positive coprime integers. Give A + B as answer.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for attention. I have same solution. Here there is fine geogebra picture - author Jerzy Mil.
Log in to reply
Fantastic! The ability to switch between views is great. Thanks for sharing it.
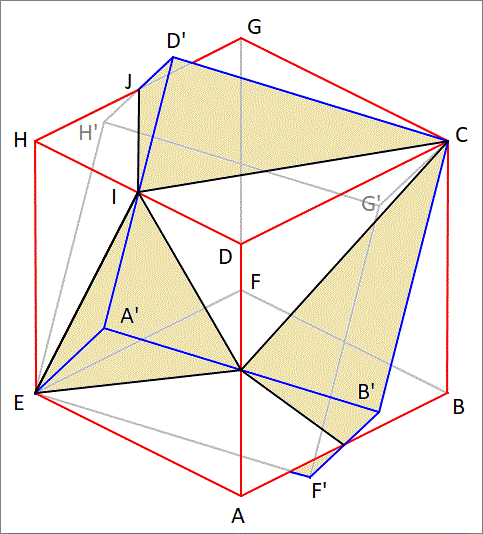
Let the two cubes have their common main diagonal between ( 0 , 0 , 0 ) and ( 1 , 1 , 1 ) . We'll keep cube 1 fixed, and rotate cube 2 by 6 0 ∘ clockwise about the axis a = ( 1 , 1 , 1 ) , the rotation matrix corresponding to this rotation is
R = ⎣ ⎢ ⎡ 3 2 − 3 1 3 2 3 2 3 2 − 3 1 − 3 1 3 2 3 2 ⎦ ⎥ ⎤
The corner of the second cube will become symmetrically on top of the top plane of the first cube. There are three planes to consider:
z = 1 (this is plane C D H G )
x = 1 (plane A B C D )
and
y = 0 (plane A D H E )
We want to determine the equation of the image of the plane z = 1 under the given rotation. Let p = ( x , y , z ) be a point on this plane, then its image is p ′ = R p = ( x ′ , y ′ , z ′ ) (because the rotation axis passes through the origin). Hence, p = R T p ′ . Now the first equation says that z = 1 , therefore, the equation governing p ′ is
− 3 1 x ′ + 3 2 y ′ + 3 2 z ′ = 1
And this is plane C D ′ H ′ G ′
Similarly for x = 1 , the equation of its image is
3 2 x ′ − 3 1 y ′ + 3 2 z ′ = 1 (this is plane A ′ B ′ C D ′ )
And finally for the plane y = 0 , its image is the plane,
3 2 x ′ + 3 2 y ′ − 3 1 z ′ = 0
(this is plane A ′ D ′ H ′ E )
We can now intersect these three planes with the plane z ′ = 1 , and this gives the base of tetrahedron I J C D ′ . It can be shown (details omitted) that the coordinates of the vertices of this tetrahedron are: I = ( 0 . 5 , 0 , 1 ) , J = ( 0 , 0 . 5 , 1 ) , C = ( 1 , 1 , 1 ) , D ′ = ( 3 1 , 3 1 , 3 4 ) . Using these coordinates one can easily determine the volume of the tetrahedron as being equal to 2 4 1 . Now, there are six of these tetrahedrons on the six faces of first cube, thus the total volume that has to be deducted from the second cube volume is 6 ⋅ 2 4 1 = 4 1 . Therefore, the common volume is 1 − 4 1 = 4 3 , and the answer is 3 + 4 = 7 .
Great solution and a beautiful problem.
This case is very symmetric. What if the angle of rotation was not 6 0 ∘ but was arbitrary? I'd be interested to know if there was a "nice" formula for the volume of intersection in terms of the angle.
Log in to reply
One could use brute force method, by finding all the intersection points, edges, and faces, of the intersection solid, and then finding its volume by segmenting it into pyramids having a common apex, which can be any point inside (or even outside) the intersection solid. This method works for any two intersecting polyhedra, with arbitrary orientation.
Thanks for attention. Here there is fine geogebra picture - author Jerzy Mil.
Given how bad my description below is, I recommend getting hold of a cube first here!
Consider a unit cube oriented with its space diagonal vertical (for example, if two opposite vertices are A and H , orient the cube so that A H is vertical). The cube has rotational symmetry of order 3 about this vertical axis (if you spin it through 1 2 0 ∘ , it still looks the same).
The second cube in this question has been rotated through half this angle. This transformation is equivalent to a reflection in the horizontal plane that bisects A H .
The section this horizontal plane makes through the cube is a regular hexagon (with sides 2 2 ) (it intersects every edge of the cube except those connected to A or H ).
The solid formed by the intersection of the two cubes is therefore a hexagonal bipyramid (ie two hexagonal pyramids stuck together at their bases); I've attempted an illustration using GeoGebra below: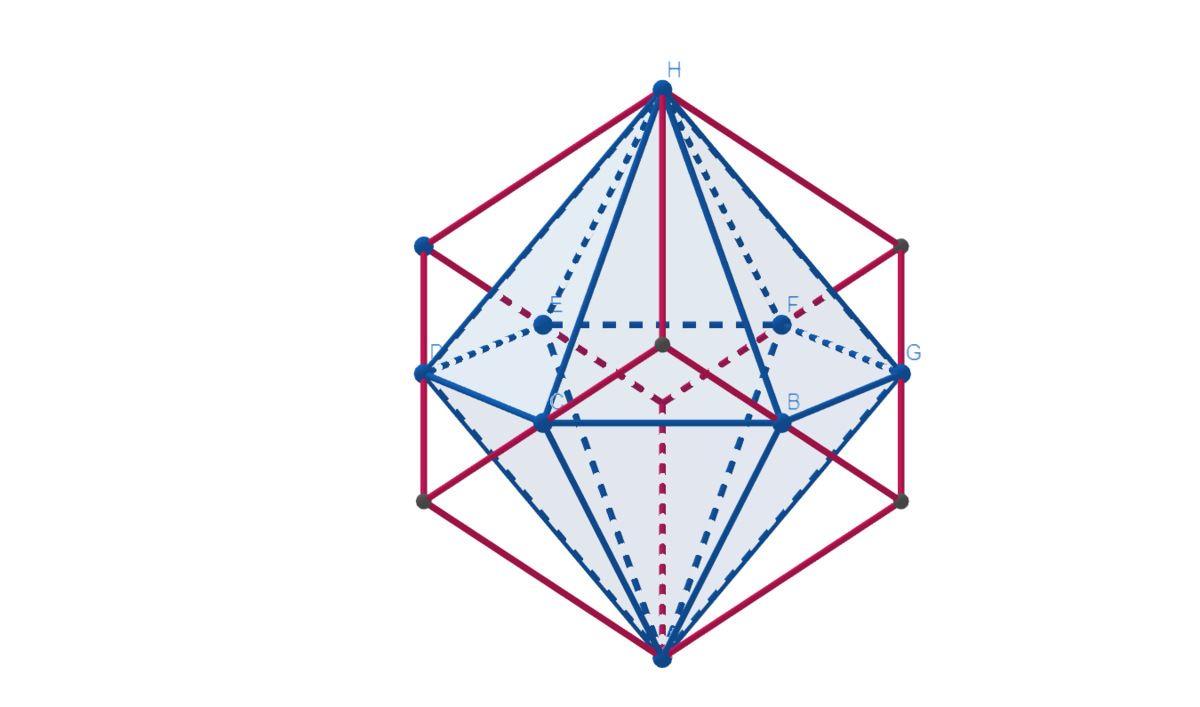
The hexagonal section of a cube is reasonably familiar, so to make computation easier we can realign the cube with coordinate axes; if A has coordinates ( 0 , 0 , 0 ) and H coordinates ( 1 , 1 , 1 ) , then the remaining vertices of the solid are the six permutations of the triple ( 0 , 2 1 , 1 ) . The intersecting plane is x + y + z = 2 3 .
We've carved off six tetrahedra, each with volume 2 4 1 , to leave a volume of 4 3 , giving the answer 7 .