Volume of a composite 3D solid

Geometry Level 5

A regular dodecahedron with unit edge length (shown in the figure below with red edges), and a regular icosahedron (blue edges) with edge length greater than 1, share the same center and are oriented in such a way that the vertices of the icosahedron all lie on the normals to the faces of the dodecahedron drawn from the centers of the faces, as the figure below illustrates. Further, the edge length of the icosahedron is such that its edges intersect the edges of the dodecahedron. Using the information below about the inradius and circumradius of both the unit regular dodecahedron and the unit regular icosahedron, find the volume of this composite solid. Use 5 significant digits to report your answer.

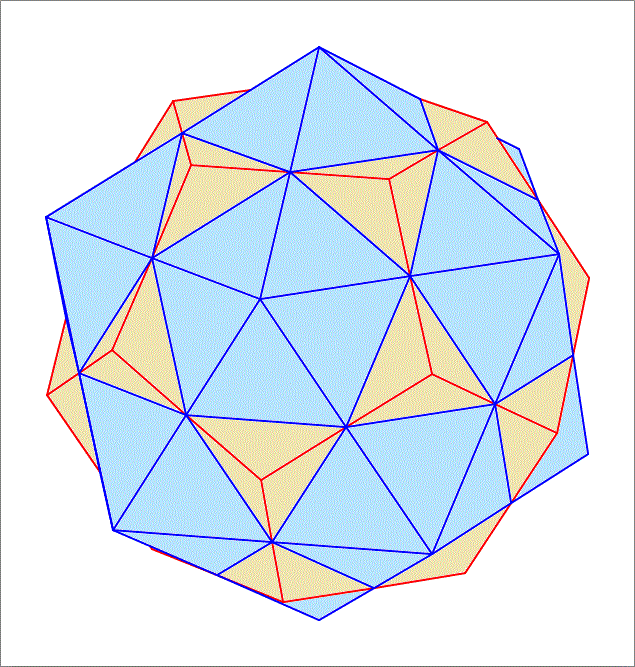
Details and Assumptions:

The inradius and circumradius of a unit regular dodecahedron are given by, respectively, $r_D = \dfrac{1}{20} \sqrt{250 + 110 \sqrt{5}}$ and $R_D = \dfrac{1}{4} (\sqrt{15} + \sqrt{3})$
The inradius and circumradius of a unit regular icosahedron are given by, respectively, $r_I = \dfrac{1}{12} (3 \sqrt{3} + \sqrt{15})$ and $R_I = \dfrac{1}{ 4} \sqrt{10 + 2 \sqrt{5}}$

The answer is 9.5789.

1 solution

Mark Hennings
Oct 16, 2018

The volume of a regular dodecahedron of side $a$ is $V_D(a) \; = \; \frac{15 + 7\sqrt{5}}{4}a^3$ while the volume of a regular pentagon pyramid of side $d$ is $V(d) \; = \; \frac{5+\sqrt{5}}{24}d^3$ This solid can be built up from a regular dodecahedron of side $1$ , together with $12$ regular pentagonal pyramids of side $\sin54^\circ = \tfrac{\sqrt{5}+1}{4}$ . Thus the total volume is $V_D(1) + 12V(\sin54^\circ) \; = \; \frac{15 + 7\sqrt{5}}{4} + 12\frac{5+\sqrt{5}}{24}\left(\frac{1+\sqrt{5}}{4}\right)^3 \; = \; \frac{5(15 + 7\sqrt{5})}{16} = \boxed{9.578898701}$

Volume of a composite 3D solid

The answer is 9.5789.

1 solution

0 pending reports