Volume of a football!
If the American NFL regulation football

has a tip-to-tip length of 1 1 inches and a largest round circumference of 2 2 in the middle, then the volume of the American football is ____________ .
Note: The American NFL regulation football is not an ellipsoid. The long cross-section consists of two circular arcs meeting at the tips. Don't use the volume formula for an ellipsoid.
Answer is in cubic inches.
The answer is 250.574.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Oh, wow, there's an "official" NFL value, given to THREE decimal places? Well I'm glad it's not exactly the same as the answer given here, otherwise people could just Google it.
Thanks for the solution, Brian. Do you know about "Daum Equation Editor"? See Daum Equation Editor
Log in to reply
Haha. Well, the "official" volume was given as 4237 c m 3 , so in my conversion I probably should have rounded it to 258.6 i n 3 . When I first attempted your question I did a Google check to see if my answer was at least in the ball park, (which it was). :)
Thanks for mentioning Daum; I played around with it a bit and it seems really useful, but my computer operating system is too ancient for me to download the app. :( However, I am slowly getting more comfortable with LaTeX; there certainly is some satisfaction in composing a "nice looking" solution, even if takes longer than I would like.
I always use Daum Equation Editor to type up solutions and questions. I don't have to worry about the rules of latex now.
Awww dang I didn't read the whole question I solved it as a prolate spheroid nice answer Brian and good question Michael
can anyone elaborate the last integral? i have tried but couldn't reach to the given answer..

In order that Brilliant can take full advantage of your solutions, I have a request. You may send the description of your sketch for the problem. I will draw the sketch and send it to you. My sketches are not of very high level of clarity but sufficient to convey the idea. Brilliant comment have no provision for sketches and I am not comfortable with other methods, I can send the sketches through attachment in e.mail. My e.mail ID is [email protected]. I draw sketches in MS PAINT with 12.5% magnification. I have the sketch of foot ball in imgur given above.
Oh god I multiply the cross sectional area along the two tips with the given circumference to get the volume without any thinking of it being so wrong and using the integral! Silly me...
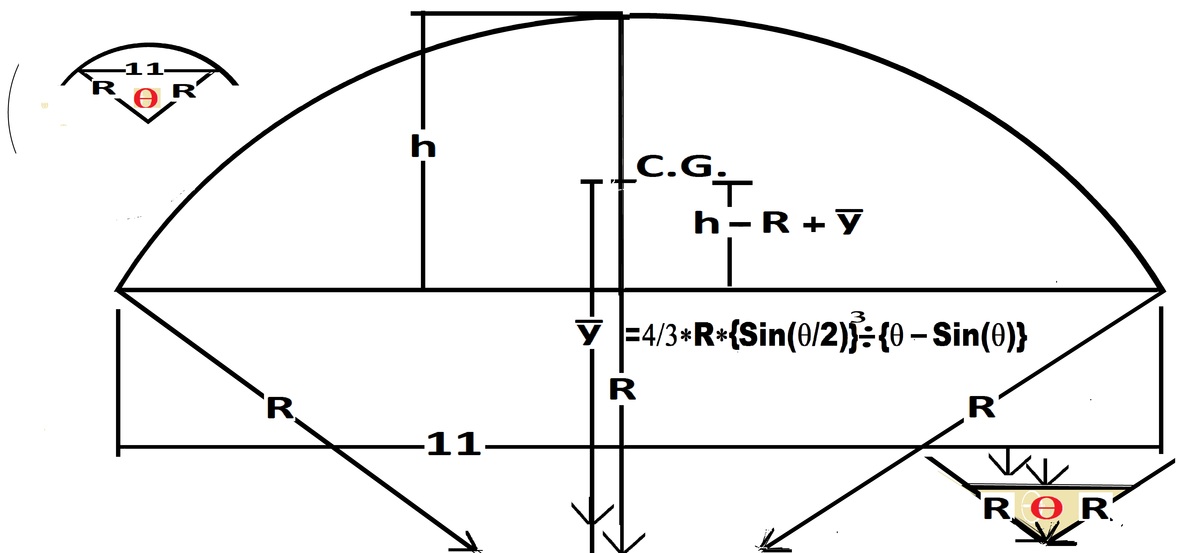
The longitudinal cross-section of the football is a segment of a circle.
The volume of revolution, V=Area to be revolved * the length of the path traced by its C.G.
Here the segment makes an angle
θ
at the center. h is the HEIGHT of the segment.
h is the radius of the maximum circle with circumference of 22.
∴
h
=
2
∗
π
2
2
=
π
1
1
The chord containing h, is divided into h, and (2R - h) by the 11" chord.
The the intersection point is the midpoint of 11" chord.
∴
h
∗
(
2
R
−
h
)
=
(
2
1
1
)
2
.
S
o
l
v
i
n
g
R
=
2
1
1
∗
π
∗
(
4
1
+
π
2
1
)
S
e
g
m
e
n
t
a
r
e
a
=
2
R
2
∗
(
θ
−
S
i
n
θ
)
From the center of the circle, C.G. is at a distance of
Y
ˉ
Y
ˉ
=
3
4
∗
R
∗
θ
−
S
i
n
θ
(
S
i
n
θ
/
2
)
3
We shall revolve the segment around the 11” chord to get the foot ball volume.
So we should have the distance of C.G. from this chord. And that distance is
r
=
h
−
R
+
Y
ˉ
N
o
t
e
R
∗
S
i
n
(
θ
/
2
)
=
2
1
1
.
∴
θ
=
2
∗
S
i
n
−
1
π
∗
(
4
1
+
π
2
1
)
1
.
C
.
G
.
t
r
a
c
e
s
a
p
a
t
h
l
e
n
g
t
h
=
2
∗
π
∗
r
.
V
=
2
∗
π
∗
r
.
∗
A
r
e
a
.
S
u
b
s
t
i
t
u
t
i
n
g
,
V
=
2
∗
π
{
h
−
R
+
3
4
∗
R
∗
θ
−
S
i
n
θ
(
S
i
n
θ
/
2
)
3
}
∗
2
R
2
∗
(
θ
−
S
i
n
θ
)
=
2
5
0
.
5
7
4
0
S i n c e t h i s i s n o t r e n d e r i n g c o r r e c t l y p l e a s e s e e b e l o w .

The longitudinal cross-section of the football is a segment of a circle.
The volume of revolution, V=Area to be revolved * the length of the path traced by its C.G.
Here the segment makes an angle
θ
at the center.
h is the HEIGHT of the segment.
...............................................................................................................................................................
h is the radius of the maximum circle with circumference of 22.
∴
h
=
2
∗
π
2
2
=
π
1
1
The chord containing h, is divided into h, and (2R - h) by the 11" chord.
The the intersection point is the midpoint of 11" chord.
∴
h
∗
(
2
R
−
h
)
=
(
2
1
1
)
2
.
S
o
l
v
i
n
g
R
=
2
1
1
∗
π
∗
(
4
1
+
π
2
1
)
S
e
g
m
e
n
t
a
r
e
a
=
2
R
2
∗
(
θ
−
S
i
n
θ
)
From the center of the circle, C.G. is at a distance of
Y
ˉ
Y
ˉ
=
3
4
∗
R
∗
θ
−
S
i
n
θ
(
S
i
n
θ
/
2
)
3
We shall revolve the segment around the 11” chord to get the foot ball volume.
So we should have r the distance of C.G. from this chord.
r
=
h
−
R
+
Y
ˉ
N
o
t
e
R
∗
S
i
n
(
θ
/
2
)
=
2
1
1
.
∴
θ
=
2
∗
S
i
n
−
1
π
∗
(
4
1
+
π
2
1
)
1
.
C
.
G
.
t
r
a
c
e
s
a
p
a
t
h
l
e
n
g
t
h
=
2
∗
π
∗
r
.
V
=
2
∗
π
∗
r
.
∗
A
r
e
a
.
S
u
b
s
t
i
t
u
t
i
n
g
,
V
=
2
∗
π
{
h
−
R
+
3
4
∗
R
∗
θ
−
S
i
n
θ
(
S
i
n
θ
/
2
)
3
}
∗
2
R
2
∗
(
θ
−
S
i
n
θ
)
V
=
3
4
∗
π
∗
(
2
1
1
)
3
−
π
∗
R
2
∗
(
R
−
h
)
{
t
h
e
t
a
−
S
i
n
θ
}
=
2
5
0
.
5
7
4
0
There seems to be some problem with Brilliant. Ignore Latex code above if it appears.
A picture would be worth a thousand words here, but since I can't provide the picture the words will have to do.
I'll start by looking at the longitudinal cross-section of the football, focusing on the "upper" region formed by one of the circular arcs and the 11-inch chord that subtends it. Now the largest round circumference of 22 inches corresponds to a radius of π 1 1 inches. This is in fact the "height" of the region we're presently dealing with, i.e., the perpendicular distance from the midpoint of the chord to the circular arc.
Now picture this arc as part of a circle of radius R centered at the origin, with the 11-inch chord parallel to and above the x-axis. Then we can form a right triangle with the origin, the midpoint of the chord and one of the chord's endpoints as vertices. Using Pythagoras, we have that
R 2 = ( 2 1 1 ) 2 + ( R − π 1 1 ) 2 .
Solving for R , we have that R = ( 8 8 ∗ π 1 2 1 ) ∗ ( π 2 + 4 ) .
Now the chord will have a y-value of d = R − π 1 1 . What we now need to do is rotate the circular arc about the horizontal line y = d to form the football as described. The radius of each of these latitudinal cross-sections will be ( y − d ) , where y 2 = R 2 − x 2 . Integrating over x , from a = − 2 1 1 to b = 2 1 1 , we then use the circular disc method to find the volume of the football. This volume is
∫ a b π ∗ ( R 2 − x 2 − d ) 2 d x .
This integral is straightforward but will involve a trig substitution, so I will just leave the reader to solve it as an exercise. The solution comes out to
π ∗ ( 1 1 ( R 2 + d 2 ) − ( 3 2 ) b 3 − 2 d R 2 ∗ arcsin ( 2 R 1 1 ) − 2 d b ∗ R 2 − b 2 ) ,
which after substituting gives us a volume of 2 5 0 . 5 7 4 cubic inches, which is within 3 % of the "official" value of 2 5 8 . 5 5 8 cubic inches.