Volume of a Part of a Cube
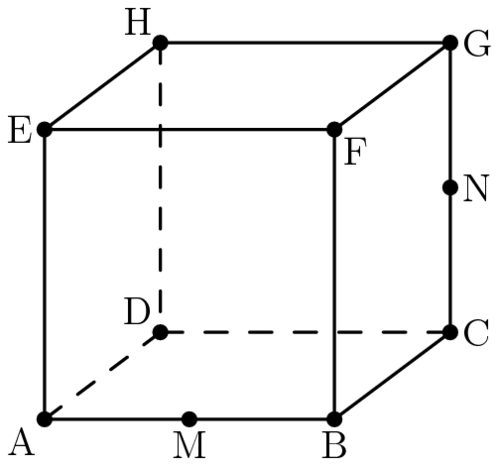 Cube
A
B
C
D
E
F
G
H
, labeled as shown above, has edge length
1
and is cut by a plane passing through vertex
D
and the midpoints
M
and
N
of
A
B
and
C
G
respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form
q
p
, where
p
and
q
are relatively prime positive integers. Find
p
+
q
.
Cube
A
B
C
D
E
F
G
H
, labeled as shown above, has edge length
1
and is cut by a plane passing through vertex
D
and the midpoints
M
and
N
of
A
B
and
C
G
respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form
q
p
, where
p
and
q
are relatively prime positive integers. Find
p
+
q
.
The answer is 89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The plane passing through D , M , N intersects F B at point X where X B = 4 1 . The smaller solid can be divided into three pyramids. If the volume formula for a pyramid is
V ( a , b , h ) = 3 1 2 1 a b h
then
V ( 2 1 , 1 , 4 1 ) + V ( 1 , 1 , 4 1 ) + V ( 2 1 , 1 , 1 ) = 4 8 7
Reorient the cube such that D is the origin and A D is the x axis. We can easily see that D M is equivalent to the line y = 2 1 x . Now note that the cross sections taken perpendicular to A D (the x -axis) are right triangles with h = 2 1 b . Setting b = 1 − 2 1 x , we get the volume as equivalent to ∫ 0 1 ( 4 1 ( 1 − 2 1 x ) 2 ) d x , which evaluates to 4 8 7 , so the volume is 1 − 4 8 7 = 4 8 4 1 , giving the final answer as 4 1 + 4 8 = 8 9 .
Call the point where the plane cuts B F , P . Now extend N P and D M until they meet at a point T . We can see that this forms a triangular pyramid. Through similar triangles we see that B P = 4 1 . We find the volume of the solid D N C B M P by finding the volume of the larger pyramid and subtracting the volume of the smaller pyramid.
The pyramids are triangular-right-pyramids, so finding the volumes is pretty straight forward.
V big pyramid = 3 2 ⋅ 4 1 = 6 1 V small pyramid = 3 1 ⋅ 1 6 1 = 4 8 1 V desired solid = 6 1 − 4 8 1 = 4 8 7
Therefore, the bigger solid is 1 − 4 8 7 = 4 8 4 1 ⟹ 4 1 + 4 8 = 8 9
The problem is from AIME. However, this should not be a level 5 problem...