Volume of a Recycle Bin

I solved using calculus. Define lengths and widths as a function of height $y$ .

$L(y) = 30 + 5 \frac{y}{30} \\ W(y) = 35 + 9 \frac{y}{30}$

The volume is:

$V = \int_0^{30} L(y) W(y) \, dy = 38625$

Since $\cfrac{30}{35} = \cfrac{35 + x}{44 + x}$ solves to $x = 19$ , we can expand the sides of $35$ and $44$ by $19$ each so that they are now $54$ and $63$ . Essentially we have now added a trapezoidal prism cross-section with a volume of $V_{\text{trap}} = \frac{1}{2} \cdot 30 \cdot (30 + 35) \cdot 19 = 18525$ , but now both pairs of parallel sides are in a $\cfrac{6}{7}$ proportion, allowing us to treat the shape as a pyramidal frustum , the difference between two pyramids.

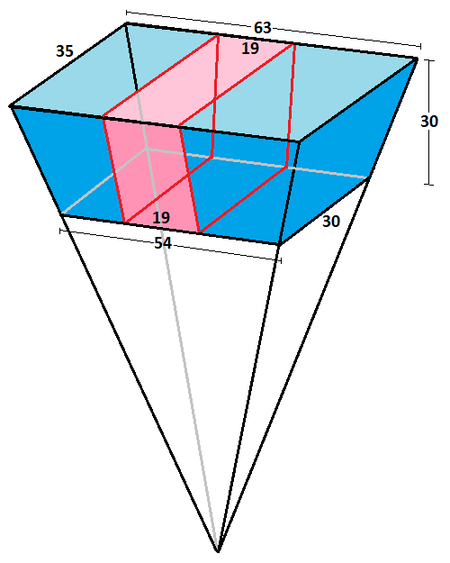
The difference in heights $h_1$ and $h_2$ of these two pyramids is $h_1 - h_2 = 30$ , and by proportions $\cfrac{6}{7} = \cfrac{h_2}{h_1}$ , and these two equations solve to $h_1 = 210$ and $h_2 = 180$ . Therefore, the volumes of the pyramids are $V_{\text{pyr1}} = \frac{1}{3} \cdot 35 \cdot 63 \cdot 210 = 154350$ and $V_{\text{pyr2}} = \frac{1}{3} \cdot 30 \cdot 54 \cdot 180 = 97200$ .

The volume of the recycle bin is therefore $V_{\text{bin}} = V_{\text{pyr1}} - V_{\text{pyr2}} - V_{\text{trap}} = 154350 - 97200 - 18525 = \boxed{38625}$ .