Volume of a Tetrahedron
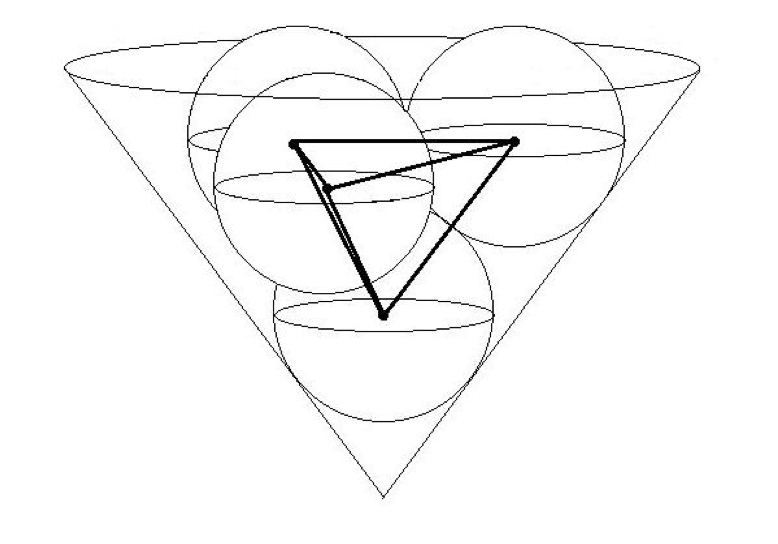
A container is shaped like a right circular cone with base diameter 18 and height 12. The vertex of the container is pointing down, and the container is open at the top. Four spheres, each with radius 3, are placed inside the container as shown. The first sphere sits at the bottom and is tangent to the cone along a circle. The second, third, and fourth spheres are placed so they are each tangent to the cone and tangent to the first sphere, and the second and fourth spheres are each tangent to the third sphere. The volume of the tetrahedron whose vertices are at the centers of the spheres is . Find
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It's hard to draw things, even 2d things! (If you're an animator, then it's an exception.) So, please try to bear with me throughout this verbose solution.
We'll try to apply the formula, V = 3 1 A h The base for the pyramid (tetrahedron in our case) will be the triangle made by the second, third and fourth sphere. We know two of its sides already. These two sides are 6 units in length. If we can find the angle (call it ϕ ) between these two equal sides, A will be known. The height will be the perpendicular distance from the first vertex (inside the first sphere) to the base. It helps to know the fact that the bases of the cone and the tetrahedron are parallel. Also, the perpendicular line connecting the first vertex to the base of the tetrahedron is a portion of the perpendicular line connecting the vertex of the cone to its base.
Finding the height is a trivial task. Similar triangles can be made from the cone and the tetrahedron. A D is the height of the cone, D E is the radius of the cone, A B = h is the height of the tetrahedron and B C = s . 6 h = 1 5 1 2 ⟹ h = 5 2 4 Now, consider the third vertex (inside the third sphere). It's distance from the perpendicular line to the base can also be calculated via similar triangle technique. This distance is s . So, 6 s = 1 5 9 ⟹ s = 5 1 8
We can find ϕ now.
Here, Q , C and P are the second, third and fourth vertices of the tetrahedron respectively. C P and C Q are 6 units each. Also, ∠ P C Q = ϕ . Additionally, the vertices P , Q and C are on a circle centered on B .
2 ϕ = arccos ( s 3 ) = arccos ( 6 5 ) You have all the ingredients now to cook up the the volume of the tetrahedron. V = 8 1 1