Volume of Cube/Cone - Part 2
A cube of unit side length is placed on the x y plane with its base centered at the origin. In addition, a right circular cone is superimposed on the cube, such that its circular base lies flat on the x y plane as well, with a diameter of 2 , and centered at the origin as well, so that the circular edge of the cone base passes through the four vertices of the cube base. The height of the cone is 2 . Find the volume of the region in space that is inside the cube but outside the cone.
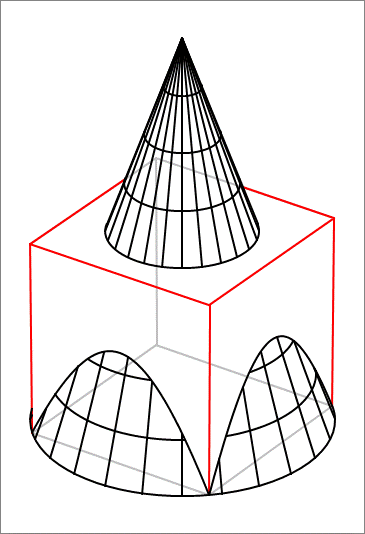
The answer is 0.213.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the third problem of this series , it was determined that the common volume to both the cone and cube is given by
V 1 = − 2 4 π + 3 4 − 3 2 ln ( 2 + 1 )
It follows that the volume of the cube lying outside the cone is given by,
V = 1 − V 1 = 2 4 π − 3 1 + 3 2 ln ( 2 + 1 ) = 0 . 2 1 3
In the animated figure 2 , M is the midpoint of A D ⌢ (assume M ∈ x ′ x ) and Z S W is the hyperbolic intersection of a plane through a point V of O M perpendicular to O M . Denote S V = h and M V = t . The triangles △ S M V , △ K M O are similar right triangles, hence, M V S V = O M O K ⇒ t h = 2 2 2 ⇒ h = 2 2 t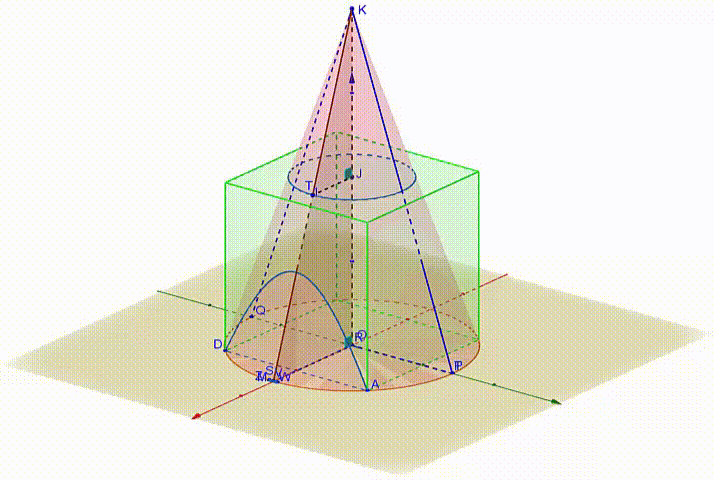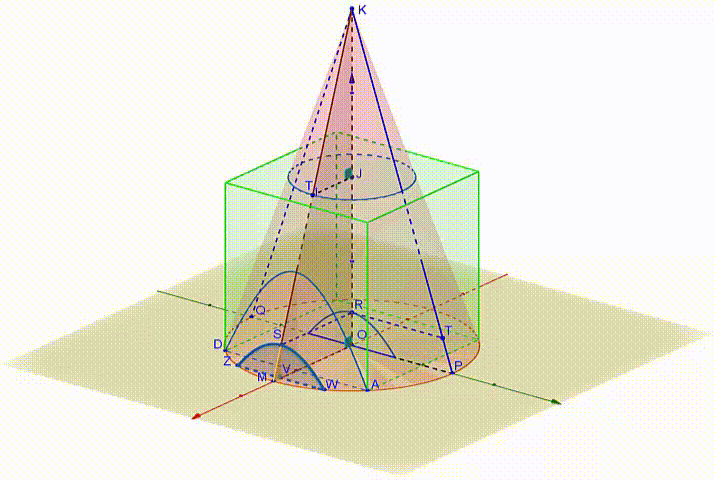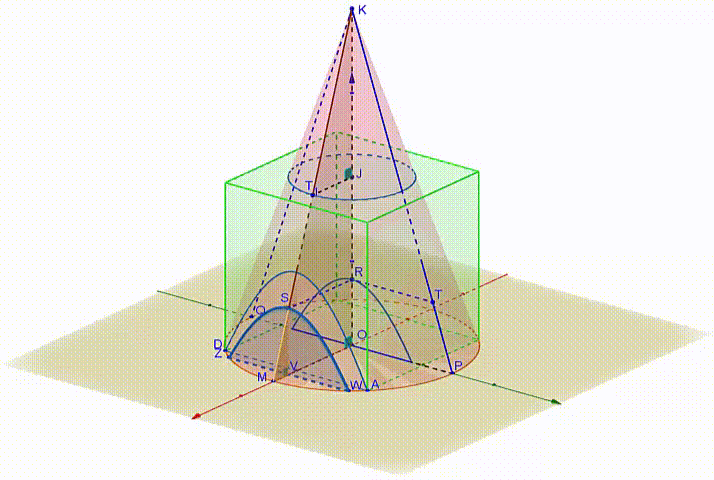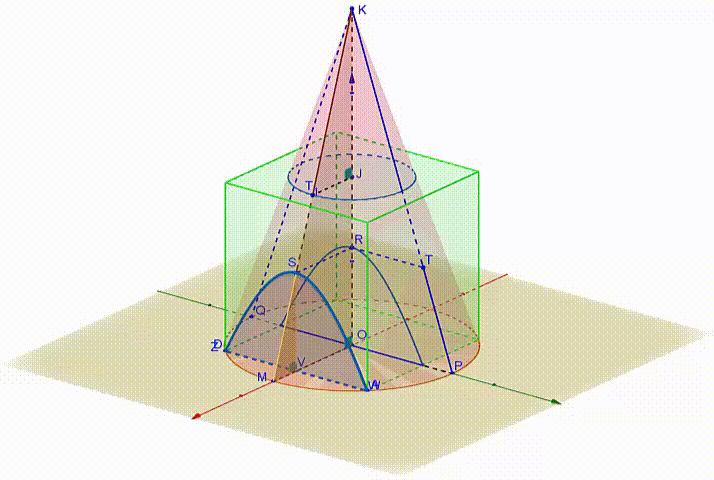 figure 2
figure 2
If we project the hyperbolic segment on the y z plane the vertex of the hyperbola is projected on point R and its asymptotes are the lines K P , K Q ( figures 2 and 3 ).
figure 3
On the y z plane, consider a 2D coordinate system with the origine at K and the line K O as the x-axis (positive direction the direction of K O ). In this setting, line l has equation x = 2 .
Moreover,
a = K R = K O − h = 2 − 2 2 t ,
b = R T = R S = O V = O M − M V = 2 2 − t
Substituting we get A = ( 2 2 − t ) ⎣ ⎡ 2 ( 2 − 2 2 t 2 ) 2 − 1 − ( 2 − 2 2 t ) ⋅ arcosh ( 2 − 2 2 t 2 ) ⎦ ⎤ Now, the volume of the cone segment is V c o n e s e g m e n t = 0 ∫ 2 2 − 1 A ⋅ d t = 0 ∫ 2 2 − 1 ( 2 2 − t ) ⎣ ⎡ 2 ( 2 − 2 2 t 2 ) 2 − 1 − ( 2 − 2 2 t ) ⋅ arcosh ( 2 − 2 2 t 2 ) ⎦ ⎤ ⋅ d t ≈ 0 . 0 3 2 3 3 6 9
Next, we go for the volume of the truncated cone.
The big cone with base on plane x y and height 2 is similar to the small one with base ( J , J T ) and height 1 . Since the rario of the heights is K O K J = 2 1 , the ratio of their volumes is 8 1 .
Hence,
V t r u n c a t e d c o n e = V b i g c o n e − V s m a l l c o n e = 8 7 × V b i g c o n e = 8 7 × 3 1 × π × ( 2 2 ) 2 × 2 = 2 4 7 π Finally, V = V c u b e − V t r u n c a t e d c o n e + 4 ⋅ V c o n e s e g m e n t = 1 − 2 4 7 π + 4 × 0 . 0 3 2 3 3 6 9 ≈ 0 . 2 1 3