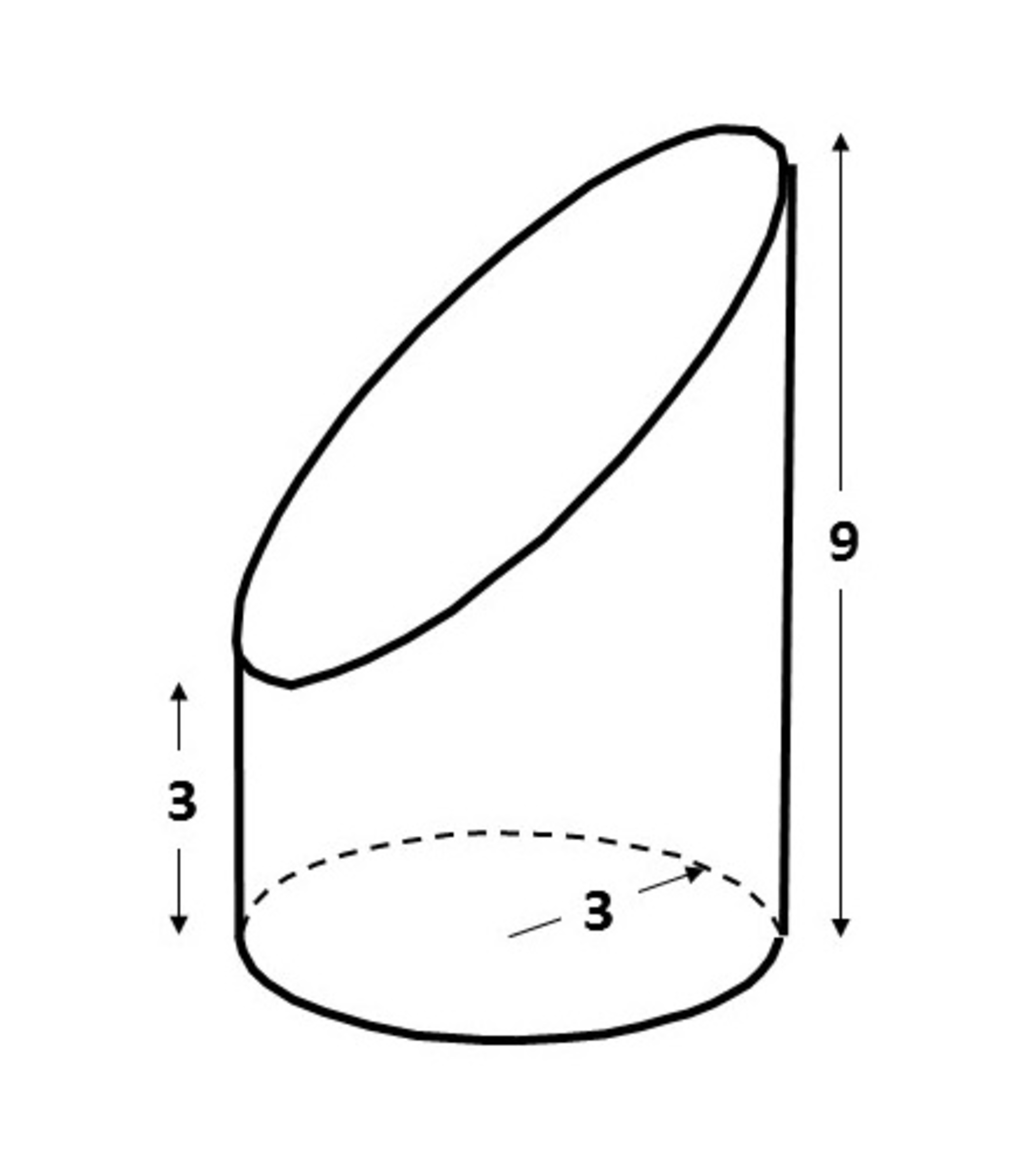
Volume of Obliquely Cut Cylinder

We note from the figure above that the top half of the obliquely cut part of the cylinder can flip over to fill up the bottom half to make a cylinder with a height of 6. Therefore the volume of the obliquely cut cylinder is $V = \pi \times 3^2 \times 6 \approx \boxed{169.65}$ .

We can use the derived formula: $V=\dfrac{\pi r^2(h_1+h_2)}{2}$ , we have

$V=\dfrac{\pi (3)^2(3+9)}{2} \approx$ $\boxed{169.65}$