Volume of sphere outside cube - part 2

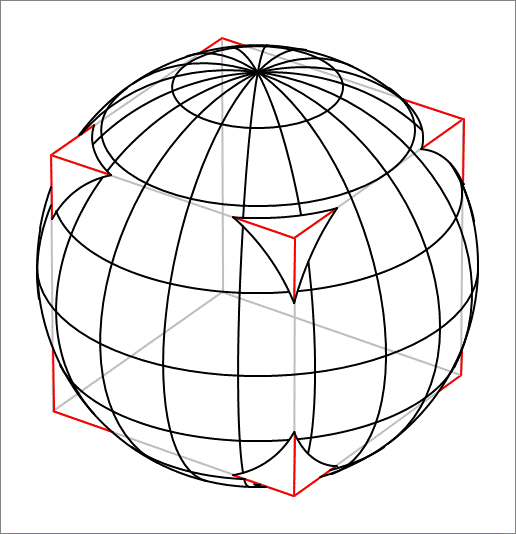
We will find the required volume indirectly by first finding the volume of the cube that lies outside the sphere. This is the volume of the 8 red corners protruding outside the sphere. Let's find the volume of one of these corners.

Define $\theta_0 = \cos^{-1} \left( \dfrac{a}{2 R} \right)$ , and $\phi_1 = \sin^{-1} ( \cot \theta_0)$ , then it was shown in the solution of this recent problem that the yellow-shaded area of the corner of the sphere is given by

$\text{Yellow Area} = A_1 = 6 R^2 \left( \cos \theta_0 (\phi_1 - \frac{\pi}{4}) + \sin^{-1} (\cos \phi_1 / \sqrt{2} ) - \dfrac{\pi}{6} \right)$

And it is straight forward to show that the green-shaded area on the face of the cube outside the sphere is given by

$\text{Green Area} = A_2 = \dfrac{a}{2} \left( \dfrac{a}{2} - r_0 \sin t_0 \right) - \frac{1}{2} {r_0}^2 \left( \frac{\pi}{2} - 2 t_0 \right)$

where $r_0 = R \sin \theta_0$ and $t_0 = \cos^{-1} \left( \dfrac{a}{2 r_0} \right)$ .

Using the yellow and green areas as found above, we can find the volume of the corners of the cube protruding outside the sphere as,

$V_1 = 8 (\dfrac{1}{3})( - R A_1 + 3 (\dfrac{a}{2}) A_2 )$

Plugging in the given values and evaluating the above formulas, we find that $V_1 = 12.40980533$

It follows that the volume of the cube that is inside the sphere (i.e. common with the sphere) is

$V_2 = a^3 - V_1 = 1000 - V_1 = 987.5901947$

And finally from $V_2$ , we get the volume of the sphere that is outside the cube as,

$V_3 = \dfrac{4 \pi}{3} R^3 - V_2 = 779.555673$

which makes the answer $\lfloor 1000 V_3 \rfloor = \boxed{779555}$