Volume of sphere outside the cube

Calculus Level 3

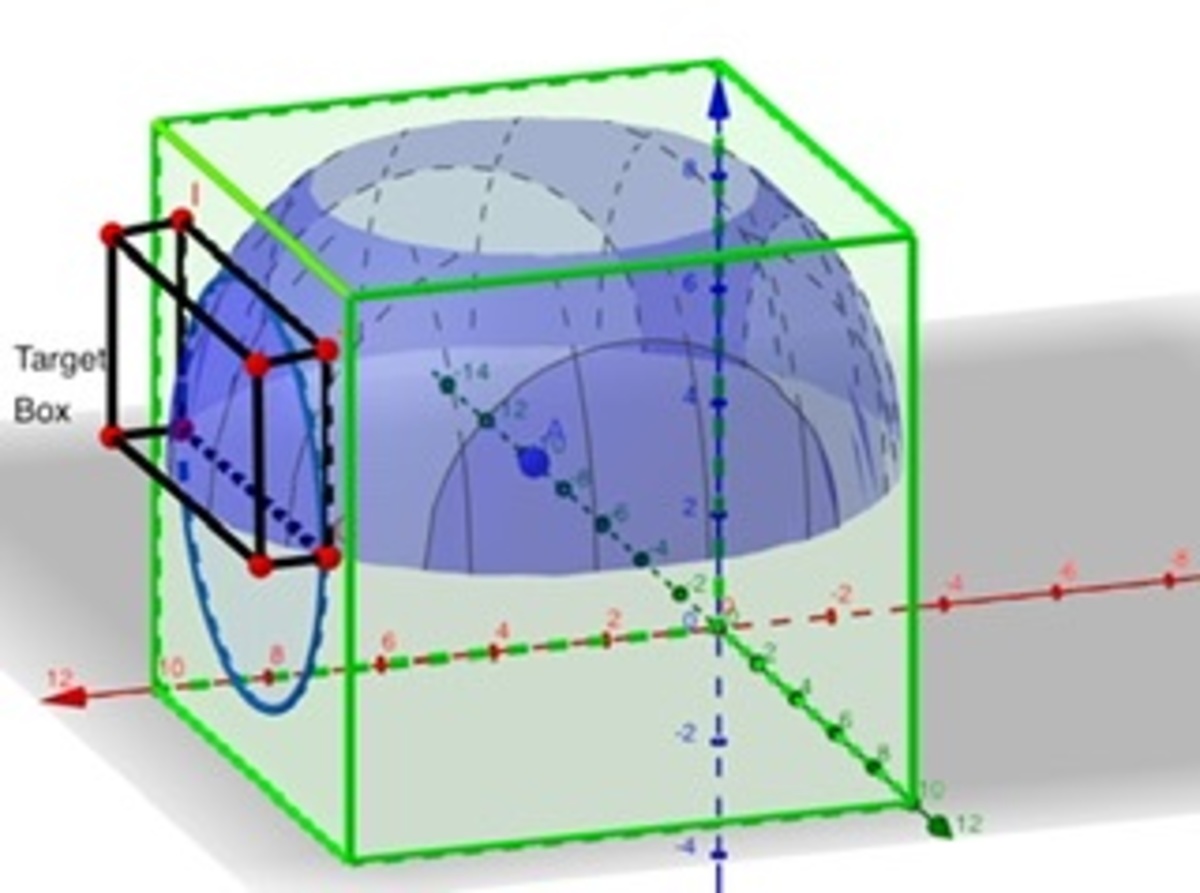
A cube of side length $10$ and a sphere having the same volume as the cube have the same center. Find the volume of the sphere that lies outside the cube.

The answer is 158.4.

3 solutions

David Vreken
Aug 7, 2020

Since the sphere and the cube have the same volume, $\frac{4}{3} \pi r^3 = 10^3$ , which solves to $r = 5\sqrt[3]{\frac{6}{\pi}} \approx 6.2035$ .

The parts of the sphere that lie outside the cube are $6$ spherical caps , which have a combined volume of

$V = 6 \cdot \frac{1}{3} \pi h^2 (3r - h) = 6 \cdot \frac{1}{3} \pi (5\sqrt[3]{\frac{6}{\pi}} - \frac{10}{2})^2 (3 \cdot 5\sqrt[3]{\frac{6}{\pi}} - (5\sqrt[3]{\frac{6}{\pi}} - \frac{10}{2})) \approx \boxed{158.4}$ .

Frank Petiprin
Oct 13, 2020

Program uses Random Points (x,y,z) to target a Box containing the volume of the sphere  outside the cube. (See Above Graph)
Import random as rd
import numpy as np
#Begin
radSph=(750/np.pi)**(1/3)
radCir=(np.square(radSph)-25.00)**.5 #Intersecting Circle With The Cube Face And Sphere (Blue circle in above Graph)
#Code to Build A Target Box Around The Sphere Outside The Box
xl1,xl2=10,radSph+5.00
yl1,yl2=5-radCir,5+radCir
zl1,zl2=5,5+radCir
boxx,boxy,boxz=xl2-xl1,yl2-yl1,zl2-zl1 #Target Box Size
volbox=boxx*boxy*boxz
seed=9021
#9015,9016,9017,9018,9019,9020
rd.seed(seed) #Turn off and on as needed for testing.
loopT=300000000 #Number of Random points tossed at target box.
countT=0
for i in range(1,loopT): # loopT is number of random tosses at the Target Box
    x,y=rd.uniform(xl1,xl2),rd.uniform(yl1,yl2)
    z=rd.uniform(zl1,zl2)
    if((x-5)**2+(y-5)**2+(z-5)**2<=radSph**2): #Is the random point on or in the sphere?
        countT+=1       
halfCirVol= (countT/loopT)*volbox #Calulate 1/2 Volume of Sphere Outside the Box for 1/2 Circle 
print('Total of hits within the sphere',countT, halfCirVol, 'Volume Sphere ',1000)
print('Volume of Targert Box',volbox)
print('Volume Of Sphere Outside The Box', 12*halfCirVol) # 6 faces on the cube 

#Total of hits within the sphere 122029082 13.201452761901567 Volume Sphere 1000
#Volume of Targert Box 32.45485226685939
#Volume Of Sphere Outside The Box 158.417433

Alexander McDowell
Aug 8, 2020

Both the sphere and the cube have the same volume. The cube has a volume of $10^3$ so the sphere must have a radius of $R = (\frac{3}{4\pi}10^3)^{\frac{1}{3}} = 6.2035$ .

For simplicity, let us look at the top of the sphere-cube and let us center the sphere and cube at the origin. We are looking for the volume within the sphere $x^2 + y^2 + z^2 = R^2$ or $r^2 + z^2 = R^2$ in cylindrical coordinates and above the plane $z = 5$ . The volume of one spherical cap is therefore $\displaystyle V = \int_{0}^{2\pi}\left(\int_{0}^{a}r\sqrt{R^{2}-r^{2}}dr\right)d\theta-5\pi\cdot a^{2}$ , where $a$ is the radius at the bottom of each spherical cap, equal to $a=\sqrt{R^{2}-5^{2}} = 3.6719$ .

Calculating $V$ yields $\displaystyle 2\pi\left(\frac{1}{3}\left(R^{2}\right)^{\frac{3}{2}}-\frac{1}{3}\left(R^{2}-a^{2}\right)^{\frac{3}{2}}\right)-5\pi\cdot a^{2} = \frac{2\pi}{3}\left(R^{3}-125\right)-5\pi\cdot a^{2} = 26.4027$ . Multiplying by six yields the total volume across all faces, $\boxed{158.416}$ .

Volume of sphere outside the cube

The answer is 158.4.

3 solutions

0 pending reports