Volume of the prism
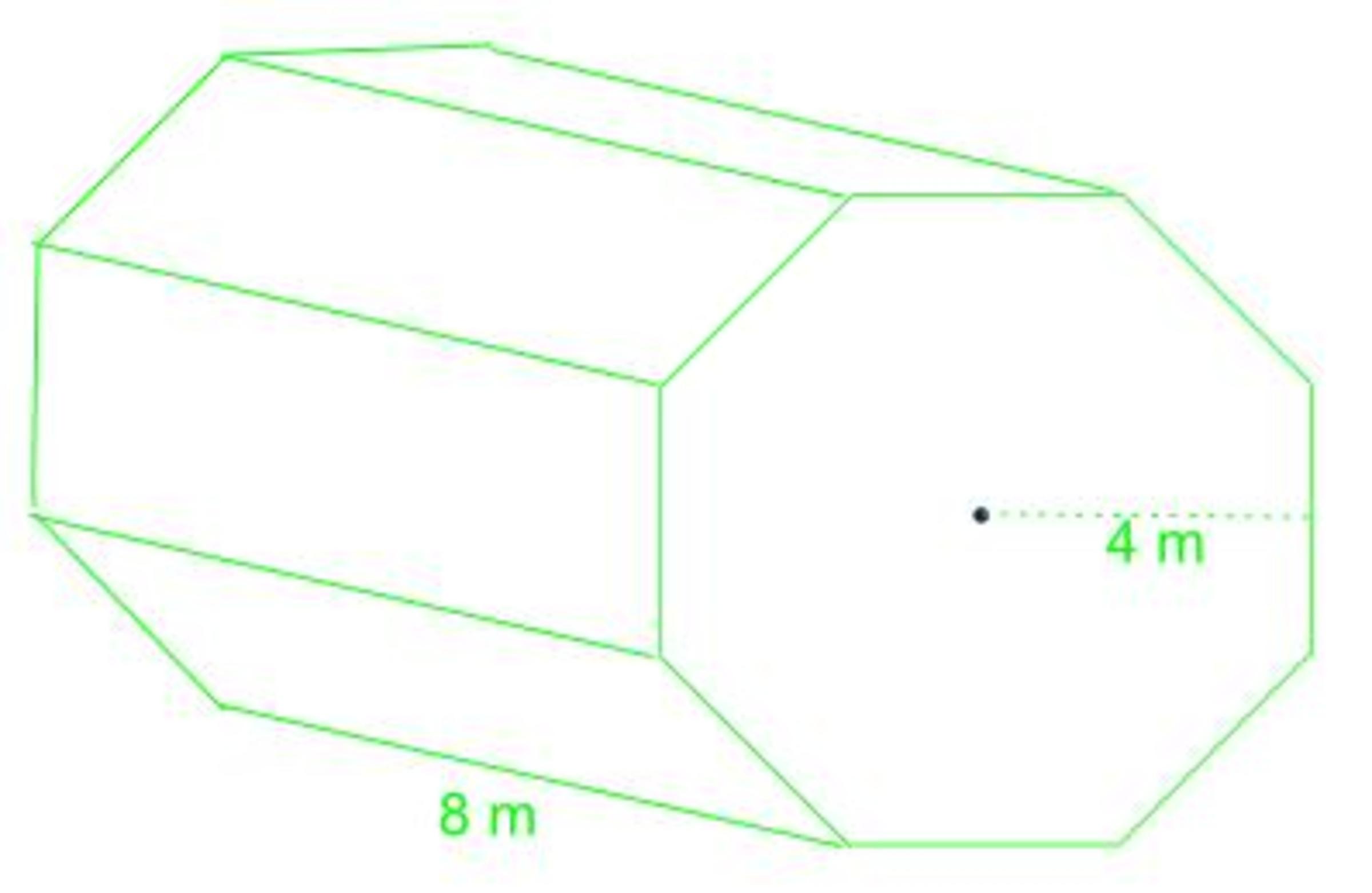
The diagram shows a prism whose cross section is a regular octagon of apothem 4 m . Its height is 8 m . Calculate the volume of the prism to the nearest m 3 .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
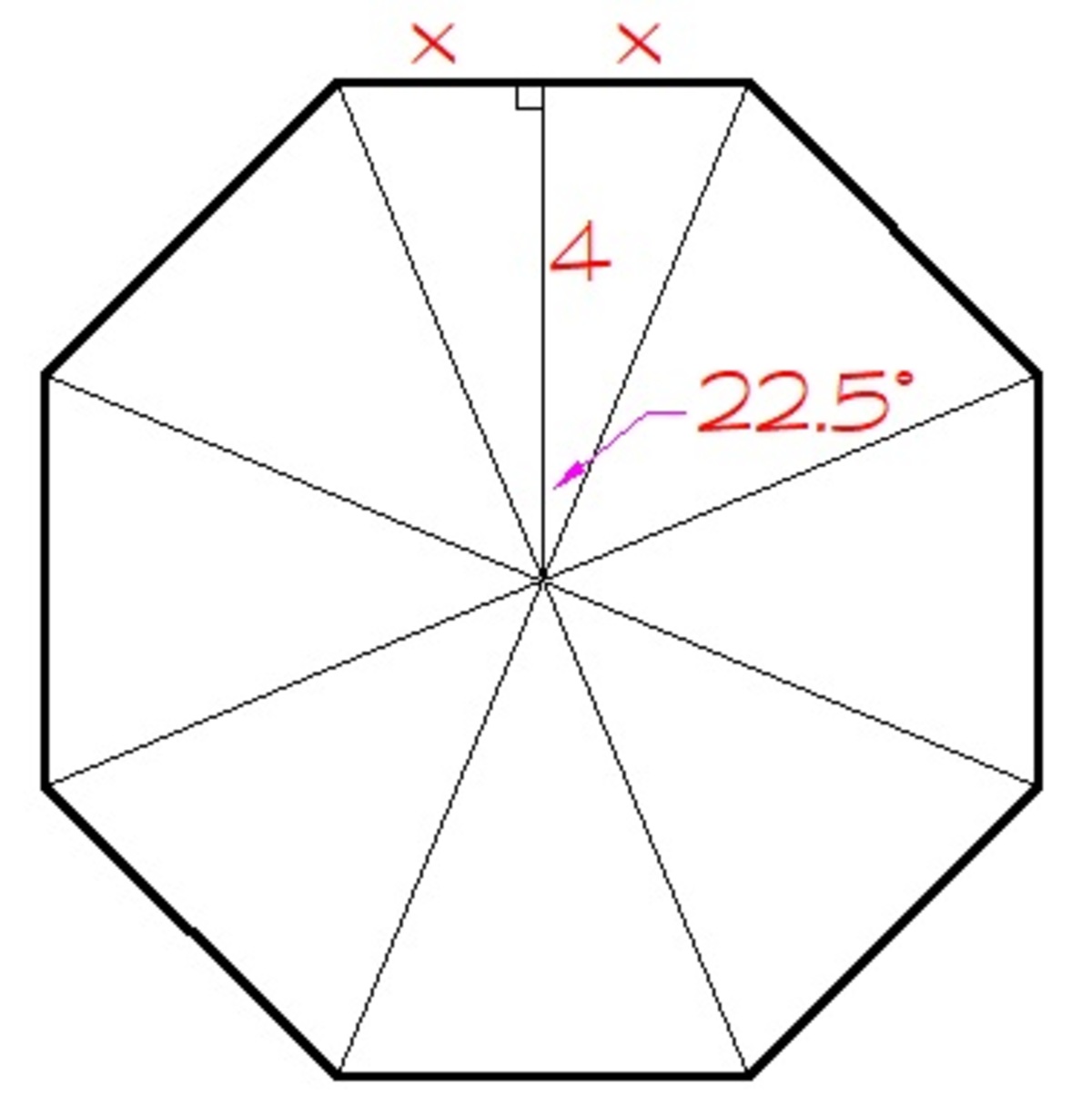 Consider the diagram.
Consider the diagram.
tan 2 2 . 5 = 4 x
x = 4 tan 2 2 . 5
2 x = 8 tan 2 2 . 5
A r e a o f t h e b a s e = 8 ( 2 1 ) ( 4 ) ( 8 tan 2 2 . 5 ) ≈ 5 3 . 0 1 9
Therefore the volume is 5 3 . 0 1 9 ( 8 ) ≈ 4 2 4
The central angle of the regular octagon θ = 8 3 6 0 ∘ . Let the radius of the circumcircle of the octagon be r . Then r = cos 2 θ 4 . And: