Volume of what remains of the cuboid
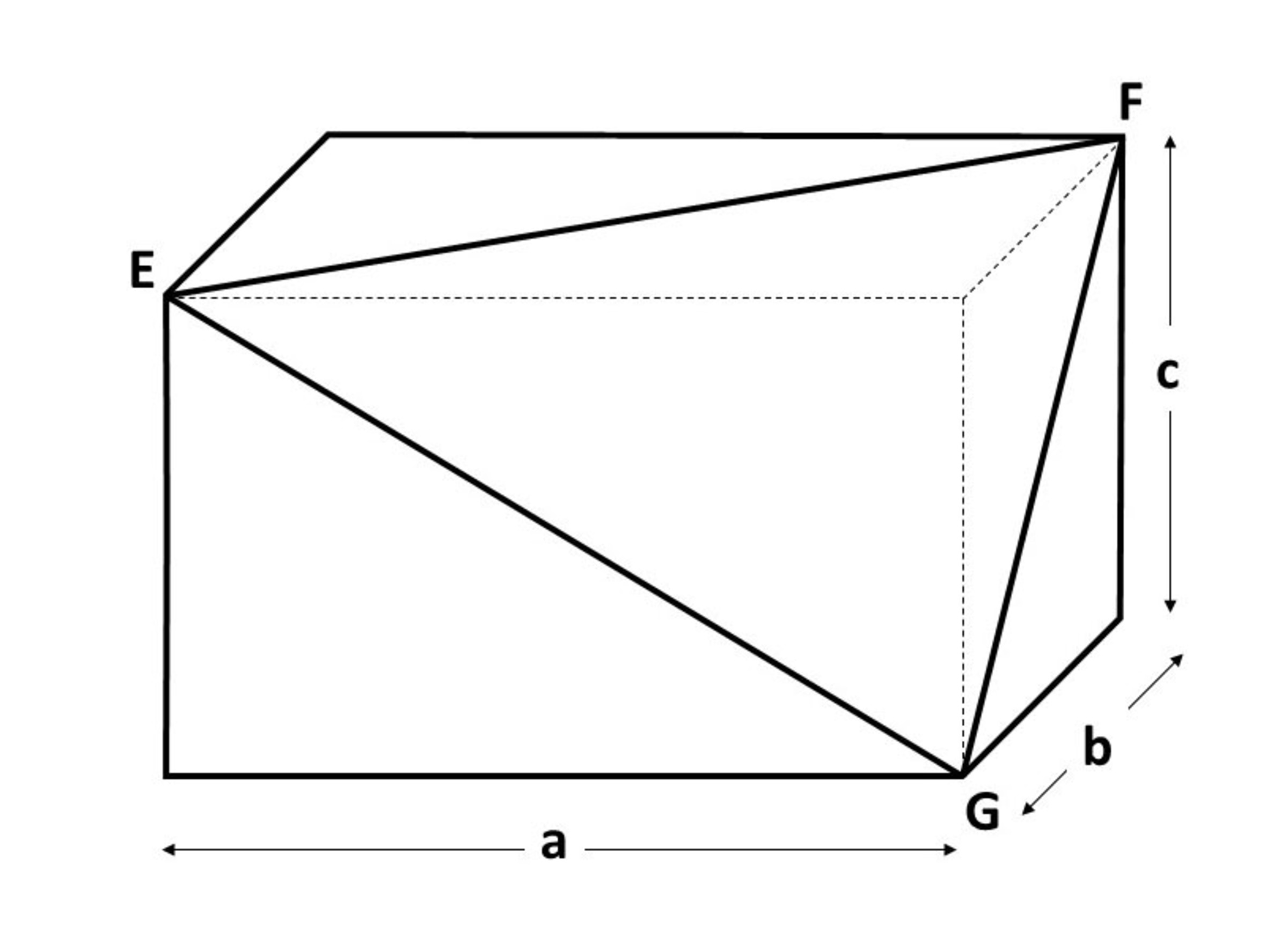
A rectangular cube (cuboid) is cut as shown, so that the cut goes through vertices
,
, and
, and the triangular pyramid is removed. What is volume of what remains of the cuboid, if
,
, and
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
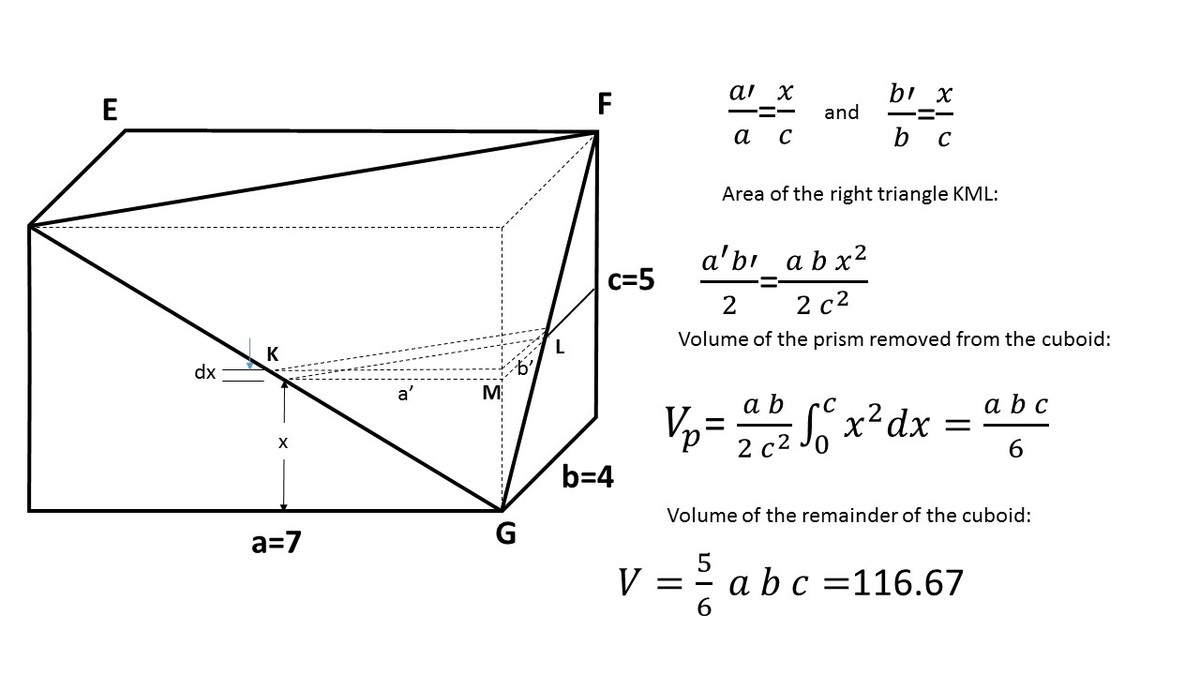
Let the vertex of the pyramid be H . The volume of the pyramid E F G H is given by:
V pyramid = 3 1 × base area × height = 3 1 × [ E F H ] × H G = 3 1 × 2 a b × c = 6 a b c
Then the volume of what remains is given by:
V remains = V cuboid − V pyramid = a b c − 6 a b c = 6 5 a b c ≈ 1 1 6 . 6 7