Weird Volume of Revolution
A region bounded by y = 2 x 2 and y = x is rotated about a line y = x . If the volume of revolution can be expressed as b a π , with a , b ∈ N and g c d ( a , b ) = 1 ,
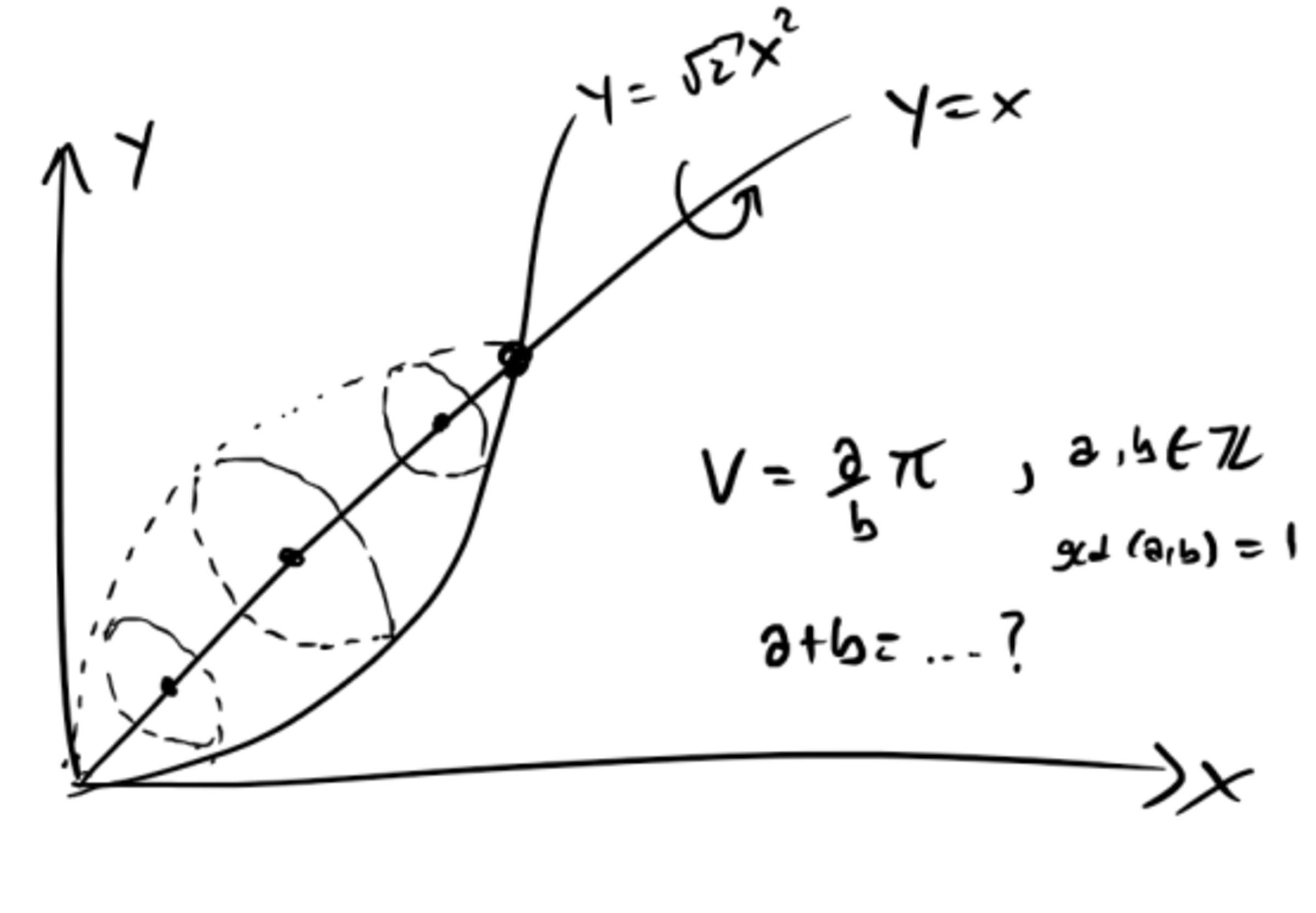
what is a + b ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The parabola y = 2 x 2 is equivalent to 2 x 2 − y = 0 , an equation in standard form where A = 2 , E = − 1 , and B = C = D = 0 . If we rotate it by 4 5 ° , then:
A ′ = A cos 2 4 5 ° + B sin 4 5 ° cos 4 5 ° + C sin 2 4 5 ° = 2 2
B ′ = 2 ( C − A ) sin 4 5 ° cos 4 5 ° + B ( cos 2 4 5 ° − sin 2 4 5 ° ) = − 2
C ′ = A sin 2 4 5 ° − B sin 4 5 ° cos 4 5 ° + C cos 2 4 5 ° = 2 2
D ′ = D cos 4 5 ° + E sin 4 5 ° = − 2 2
E ′ = − D sin 4 5 ° + E cos 4 5 ° = − 2 2
for a new equation of 2 2 x 2 − 2 x y + 2 2 y 2 − 2 2 x − 2 2 y = 0 , which rearranges to y = x + 2 1 − 2 1 8 x + 1 .
The line y = x rotates to y = 0 after a 4 5 ° rotation, which intersects y = x + 2 1 − 2 1 8 x + 1 at ( 0 , 0 ) and ( 1 , 0 ) .
The volume is then V = ∫ 0 1 π ( x + 2 1 − 2 1 8 x + 1 ) 2 d x .
Substituting u = 8 x + 1 and rearranging gives V = ∫ 1 3 2 5 6 π ( u 5 − 8 u 4 + 2 2 u 3 − 2 4 u 2 + 9 u ) d u = 1 2 0 1 π .
Therefore, a = 1 , b = 1 2 0 , and a + b = 1 2 1 .
The intersection of the two curves is at x = 2 x 2 , which is at x = 0 and x = 2 1 . Given a point ( x , 2 x 2 ) on the parabola, its perpendicular distance to the line y = x is given by
r = 2 1 ( x − 2 x 2 )
The thickness of the disc is 2 d x , hence the volume is given by
V = ∫ 0 2 1 2 π r 2 d x
Plugging the expression for r from above, we get
V = 2 ∫ 0 2 1 π 2 1 ( x − 2 x 2 ) 2 d x
Expanding, and integrating, this becomes,
V = 2 2 π ∫ 0 2 1 ( x 2 − 2 2 x 3 + 2 x 4 ) d x
V = 2 2 π ( 3 1 ( 2 1 ) 3 − 2 2 ( 1 / 2 ) + 5 2 ( 2 1 ) 5 )
V = 2 1 π ( 6 1 − 4 1 + 1 0 1 ) = 2 1 π ( 6 0 1 ) ( 1 0 − 1 5 + 6 ) = π ( 1 2 0 1 )
So that a = 1 , b = 1 2 0 , making the answer 1 + 1 2 0 = 1 2 1 .