Volume Ratio

Setting height equal to $1$ will make the radius $R=\sqrt{2}$ .

The cube will be largest when in contact with the cone. One of the top vertices of the cube, $D$ , will be the length of the edge of the cube, $a$ , off the ground and half the diagonal of the top face of the cube from the centerline $EA$ . As we can see in the top view of the level of the top of the cube:

From Pythagorean theorem $CD=\sqrt{(\frac{a}{2})^2+(\frac{a}{2})^2}=\frac{\sqrt{2}a}{2}=\frac{a}{\sqrt{2}}$ .

Triangles $ECD$ and $EAB$ are similar, so $\frac{\sqrt{2}}{1}=\frac{\frac{a}{\sqrt{2}}}{1-a}$ .

Solving for $a$ : $a=\frac{2}{3}.$

So the volume of the cube: $V_{cube}=\frac{8}{27}$ .

Volume of the cone: $V_{cone}=\frac{\pi R^2}{3}=\frac{2\pi}{3}$ .

The ration is then $\frac{9\pi}{4}\approx7.065.$

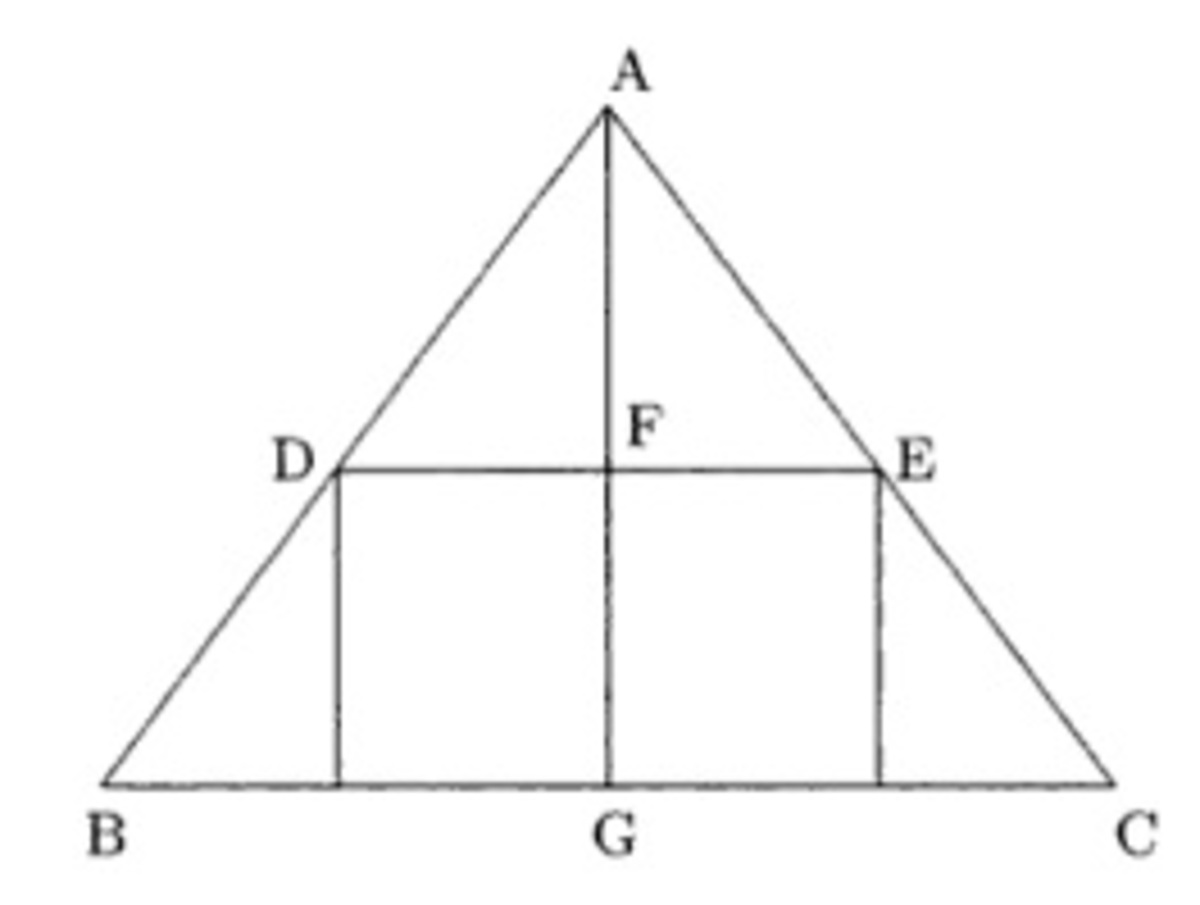
Consider a plane cross-section through a vertex of a cube and the axis of the cone as shown in the figure. Let $s$ be the side length of the cube. Segment $DE$ is a diagonal of the top of the cube. By applying Pythagorean Theorem, its length is $s\sqrt{2}$ . From the similar triangles $ADE$ ~ $ABC$ we have, $\frac{DE}{BC}=\frac{AF}{AG}$ , or equivalently $\frac{s\sqrt{2}}{2r}=\frac{h-s}{h}$ . After simplifying, we get $s=\frac{2}{3}h$ .

Now take the ratio of their volumes.

Solving for the volume of the cone

In the problem, it states that $r=\sqrt{2}h$ and $pi=3.14$

$V_{cone} = \frac{1}{3}A_{base}h = \frac{1}{3}(3.14)(\sqrt{2}h)^2h=\frac{1}{3}(3.14)(\sqrt{2})^2h^3=2.093333333h^3$

Solving for the volume of the cube

$V_{cube} = s^3=$ $(\frac{2}{3}h)^3$ $= 0.296296296h^3$

Taking the ratio of their volumes

$ratio=$ $\frac{2.093333333h^3}{0.296296296h^3} =$ $\boxed{7.07}$