Wait! What Weights
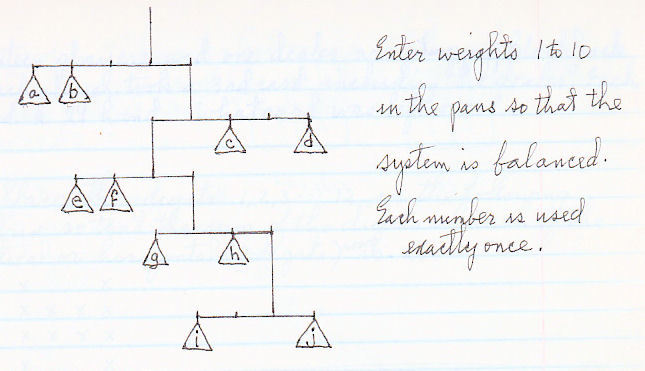 The system is balanced with weights from 1 to 10 in each pan. Each number is used only once.
The system is balanced with weights from 1 to 10 in each pan. Each number is used only once.
What is the sum of the weights placed in pans e, f, and g?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Discussions for this problem are now closed
I dont get it.For a case ,the sum of weights on the right side of weigh balance should always be equal to the left...Isn't it ? Otherwise it would hang on one side..SO,A+B should be equal to C+D+E+F+G+H+I+J...please thell me where am i wrong?As this case is not possible without repetition..
Sum of weights isn't the only thing that is important, the distance from the pivot (the pivot of the bar that the weights are hanging on) is also important. E.g. imagine holding a long ruler. A weight that is close to your hand is going to 'feel' less heavier than a weight at the far end of the ruler.
What actually needs to be equal on both sides is the weight x distance from the pivot point.
We can see that A is three parts away from the pivot, and B is two parts away from the pivot. Meanwhile, everything else acts one part away from the pivot. Thus, 3a + 2b = c+d+...+j (and so on). Hope this helps!
No...the balance does not just depend on the weights but their moments i.e. the product of the weight with the distance of the point of suspension of the weighy from the pivot.
even if i = 1 and j = 2, how are you going to balance g = h + 2(4) when g cannot take more than 10 and h can not take already used values
i also think like this~the value up there will become very high~
to balance i and j, you need to use the torque 2i = j but it's weight should be W = i + j
i am confused with
g=h+2(i+j) or g=h+2(2i+j)
i is 2 unit far from pivot
In the first equation g=h+2(i+j) g=h because they are equal distances from the pivot, but the combined weight of i and j are twice as far from the pivot therefore its force downward is doubled (law of levers).
The second equation is incorrect. Where did you get it from?
It should be g=h+2(i+2i) obtained by substitution.
Using the equilibrium condition (Summation of moments equal to zero), we can create equations for each section and the corresponding weight caused on the above section. Interpreting the values, the only condition is: a=10, b=5, c=8, d=6, e=4, f=7, g=9, h=3, i=1, j=2. Therefore, the answer is e+f+g=4+7+9=20
SIR CAN U MAKE IT CLEAR PLEASE ITS REALLY WONDERFUL ??????????????
What do you want cleared up?
10 on a 3 unit arm plus 5 on a 2 unit arm is equivalent to 40 on a 1 unit arm, etc.
Can you explain how we can deduce this solution set?
I see 5 equations from balancing at the fulcrums. Do you then check it case by case?
Well technically there are infinite solutions if one does not consider the constrains. Now applying the constrains and using optimizatuon techniques, one can determine the possible values of some variables eg. 'i'. Then continue to solve
It is obvious that the higher you go up the heavier the mass u require to balance the torque equations. So if we need to assume any 2 sets of values for the bottom most arm it should be 1 and 2. Any other values will make the upper arm unbalanced. From there on we just have to solve the torque equations of each arm.
"there are only two sets.." how did you know that?
Because by substituting integrals 1 to 10 into the a for equation 4a + 3b = 55 you only get integrals value for b when a is 7 or 10
why g = h + 2(i + j)
You need to know how torque works before working on this question. It is easier to work from bottom to the top. By simple inspection, the bottom weights i and j can only be 1 and 2 respectively, because the weight g cannot support any values larger than that. The next step is to determine g and h. The only possibilities are (g=9, h=3) or (g=10, h=4) as h cannot be higher since g cannot bear a value higher than 4 for h, and other values like 1 and 2 are used up in i and j weights. You have to assume one of the values for g and h and work upwards in the same reasoning and you'll eventually get the values for all the weights.
SPOILER: a=10, b=5, c=8, d=6, e=4, f=7, g=9, h=3, i=1, j=2
You sir are absolutely spot on.
Brilliant and Thanks for avoiding equations!!
Maybe Reasoning is the quickest way to solve this- as it avoids complex math equations! But you need to have the basic concept of Physics...
Bottom fulcrum 2i = j
4th fulcrum g = h+2(i+j) = h+3j since g <= 10, then j <= 3 and from 2i = j, j has to be even number, so we have j = 2 and i = 1 and we have g = h+6, h <= 4 since 1 and 2 are used, h = 3 or 4 and g = 9 or 10
3rd fulcrum 2e+f = g+h+i+j = g+h+3 = 2h+9 2(e-h) = 9-f so f <9 and has to be odd number (5 or 7)
Top fulcrum, we have 2 equations
3a+2b = c+d+...+j = 55 - (a+b) --> 4a+3b = 55 2 possibilities; a = 10, b = 5 or a = 7, b =9 and 3a+2b = 2c+4d = 2(c+2d) so a has to be even number (10 only) Finally, we have b = 5, g = 9 (10 is used), h = 3, f = 7 (5 is used) and for 2e+f = 2h+9 --> we have e = 4
e+f+g = 4+7+9 = 20
why 2e+f = g+h+i+j or g = h+2(i+j)
Brute force in Python! Mainly because this was giving me a headache.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
solve the problem from the bottom...
at the 5th level (bottom) we have 2i = j
at the 4th level we have g = h+2(i+j) <-(i,j assumed as one element)
at the 3rd level we have 2e+f = (g+h+i+j)
at the 2nd level we have c+3d = (e+f+g+h+i+j)
at the 1st level we have 3a+2b = (c+d+e+f+g+h+i+j)
the first equation you must to solve is the 5th level equation as the bottom of system because when we solve (the equation is balanced) the bottom we can ignore it (is it balanced or not) in the next equation above it, just sum up all of the weight in previous level and assume it as one element in the next equation
so, because the bottom level equation is
2i = j
we only have 5 possibilities
1) i=1,j=2
2) i=2,j=4
3) i=3,i=6
4) i=4,i=8
5) i=5, i=10
try the smallest possible number first
you have to put the smallest possible number first in the farthest place from pivot (torque effect)
so, try the first pair..and ...
5th)
i=1,j=2
4th)
g = h+2(i+j)
g = 3+2(1+2) <- the smallest possible number is 3
9 = 3+2.3
g=9,h=3
3rd)
2e+f = g+h+i+j
2.4+f = 9+3+1+2 <- i put 4(the smallest possibility) in the farthest place from pivot)
8+f = 15
e=4,f=7
2nd)
c+3d = e+f+g+h+i+j
c+3d = 4+7+9+3+1+2
c+3d = 26
the only possible number: c=8,d=6
1st)
3a+2b = c+d+e+f+g+h+i+j
3a+2b = 8+6+4+7+9+3+1+2
3a+2b = 40
the only possible number is 10 and 5...
a=10,b=5
SOLVE!
so, now the answer...
e+f+g = 4+7+9=20
why not g=h+2(2i+j)
1) first separate the given numbers into two groups which are equal..
what i did was through trial and error. 9 , 7 , 6 , 3 , 2 = 10 , 8 , 5 , 4
2) the next step was to arrange all the available spots for the masses on straight balancing bar.. where some points on the bar would take two sets of masses.
3) then, again by trial and error i moved the masses around and calculated its moment about the hanging point. (pivot)
-
moment on right side + (10) x 1 + ( 7 + 2 ) x2 + (1 + 3 ) x 4
-
moment on left side - ( 4) x 3 - ( 8 + 5) x 2 - (6) x 1
-
the weight at the balancing point itself has no moment, perpendicular distance from pivot = 0 . also i took a clockwise rotation as positive and anticlockwise as negative.
the resultant moment is 0 , therefore the system is balanced
Lets look at all the equations- 1)j=2i 2)g= 2(i+j)+h 3)2e+f=g+h+i+j 4)3d+c=e+f+...+j 5)3a+2b=c+d+...+j
(i)i and j cannot be greater than 1 and 2 because this is the maximum (and only)value for which g is <=10..so i=1 and j=2
(ii)only values satisfying equn 2 (after putting the values of i and j) are g=7 and h=1 and g=9 and h=3..but since 1 is already used g=9 and h=3
(iii) only values satisfying equn 3 ----2e+f= 15 (after putting g,h,i,j) are e=4 and f=7 This part is enough to get the answer (20) but i am gonna find out all of the values to verify the results
(iv) the only values that satisfy the equn4 ---3d+c=26 are 6 and 8 so d=6 and c=8
(v) that leaves us with two no.s 10 and 5 and putting them in the equn 5 we get 30 + 10=6+8+26...s o we can see that the equn is satisfied and so the values are correct..
So the answer id e+f+g=4+7+9=20
10, 5, 8, 6, 4, 7, 9, 3, 1, 2
Here's the reasoning:
55 = a+b+c+...+h+i+j
3a + 2b = c+d+...+h+i+j
55 = a+b+3a+2b
55 = 4a+3b
There are only 2 sets of integral values for a and b, namely (7,9) and (10,5)
From the bottom end
g = h + 2(i + j)
j = 2i
g = h + 2(i + 2i)
g = h + 6i
There's only 1 possible value for i , namely 1. Thus j = 2.
Only possible values for g and h are 10 and 4 or 9 and 3. Carry on....