Wali's Number
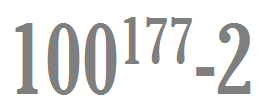
Find the sum of all the digits of the number above when it is stated in decimal representation.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
For the sake of users who weren't familiar with that formula, they can even work out the problem as follows.
Observe that 9 9 9 . . . n 9 9 … 9 = = = 1 0 − 1 1 0 2 − 1 1 0 n − 1
Thus, we can write the given expression as 1 0 0 1 7 7 − 2 = 1 0 3 5 4 − 2 = ( 1 0 3 5 4 − 1 ) − 1 = 3 5 4 9 9 … 9 − 1 = 3 5 3 9 9 … 9 8
Thus sum of digits of above number would be 3 5 3 × 9 + 8 = 3 1 8 5
EDIT : Thus, you can even work out for the general formula of sum of digits of : 1 0 n − m where n ∈ N and 0 ≤ m ≤ 9 as follows 1 0 n − m = n 9 9 … 9 − m + 1 Thus, sum of digits will be 9 × ( n − 1 ) + ( 9 − ( m − 1 ) ) = 9 n − m + 1 S ( 1 0 n − m ) = 9 n − m + 1
Log in to reply
in response to @Kishlaya Jaiswal actually you did the same What I did but yes your answer is a detailed answer for those who want to know the concept of how I got the formula.Even I thought to upload the complete answer but I thought it would have been too long but it's good that u uploaded it. :)
See, 100^177 has (177 X 2) 0's = 354 0's and a 1. If you subtract 2, you get 353 9's and a 8. 353 X 9 = 3177 and added with 8 , it becomes 3185.
while practicing such type of question i found out the formula for solving the questions of the form 10^n-2 the formula is [(x-1)n-1] ;where x denotes 10 n denotes the power of 10 implies = 100^177-2={(10)^2}^177-2=10^354-2 now using my formula, (x-1)n-1=(10-1)354-1=3186-1=3185 if you want to understand how I deduced the formula then u can reply and I will be sending u the complete way of solving these type of questions. Hope it helped u to some extent. :)