Walking Across a Chess Board

First of all, let's turn our chess board into the first quadrant of a two-dimensional graph with an $x$ and $y$ axis. Bobby starts at the bottom left corner so we'll label his starting point as $(0,0)$

Secondly, let's determine a function $S(a,b)$ that gives us the number of squares that a line of the form $y=\frac{a}{b}x$ will cross.

We must first notice that the smallest number of squares that any line will cross is $8$ ; there are 8 columns therefore the line must at least pass through $1$ square in each column. We now know that our function must take the form $S(a,b)=8+X$

What happens when each of these lines pass from one square to another? For this there are two cases we must consider. A line can either enter another square by crossing over an edge or by crossing through a corner. Let's start with the first case.

How high does Bobby walk? We were given the condition $0<a<b\leq10$ , meaning that $\frac{a}{b} < 1$ . This means that Bobby will be traveling below the diagonal of the board. Asking how high Bobby will walk is the same as asking what is the value of $y$ when $y=\frac{a}{b}x$ . If $x=8$ , the width of our chess board, then $y=\frac{8a}{b}$ . Let's say for example that $y=\frac{7}{10}x$ , therefore $y=\frac{8(7)}{10}=5.6$ That means that the line will have crossed 5 rows of the chess board and ended in the 6th. We know that our slope is less than 1, so there's no way that our line can pass through more than one square per column. Either our line simply crosses into the next column, or it passes first through the square above it and then enters the next column. Our example line $y=\frac{7}{10}x$ ends in the 6th row, meaning that it had to pass through 5 extra squares on its pass through the 8 columns, assuming that it always passed through an edge and not a corner. Taking our function into account, we know that the maximum number of squares that our line can cross is $S(a,b)=8+\lfloor\frac{8a}{b}\rfloor$ , where $\lfloor x \rfloor$ denotes the floor function, a function that returns the greatest integer less than or equal to $x$ . For example, $\lfloor 4.372 \rfloor\ = 4$ .

But like I said before, there are two cases. What the line crosses through a corner and not an edge? Every time that the line passes through a corner we must subtract $1$ from our answer. This too can be written in closed form by using the floor function. We're looking for when $y$ is an integer between in the interval $[0,8]$ Let's use the line $y=\frac{2}{3}x$ as our example this time. Every 3 columns this line will cross a corner because $\frac{2}{3} (3n) = 2n$ . How many times is this particular $y$ an integer when $0\leq x \leq 8$ ? One can observe that the answer to this question is $\lfloor \frac{8}{b} \rfloor$ . If we subtract this value from our maximum value of $S$ to get our final value for the function:

$S(a,b) = minimum$ $value+rows$ $crossed-corners$ $crossed$ $through$

$S(a,b) = 8+\lfloor\frac{8a}{b}\rfloor-\lfloor\frac{8}{b}\rfloor$

Now we're getting somewhere! Our question asks when does $S(a,b)=12$ for values of $a,b$ where $0<a<b\leq10$ . Plugging in for $S$ we get:

$12 = 8+\lfloor\frac{8a}{b}\rfloor-\lfloor\frac{8}{b}\rfloor$

$4 = \lfloor\frac{8a}{b}\rfloor-\lfloor\frac{8}{b}\rfloor$

Since both $\lfloor\frac{8a}{b}\rfloor$ and $\lfloor\frac{8}{b}\rfloor$ are positive, this gives us a few conditions that we can work with to find solutions to our problem. Our conditions come from supply different values of $b$ .

If $b = 2$ :

$\lfloor\frac{8}{b}\rfloor = 4 \Longrightarrow \lfloor\frac{8a}{b}\rfloor = 8$

$\lfloor\frac{8a}{2}\rfloor = \lfloor 4a\rfloor=8 \Longrightarrow a = 2$

$a$ can't be two because this fails $a<b$ and the fact that $a$ and $b$ are coprime.

If $3 \leq b \leq 4$ :

$\lfloor\frac{8}{b}\rfloor = 2 \Longrightarrow \lfloor\frac{8a}{b}\rfloor = 6$

$6 \leq \frac{8a}{b} \leq 7 \Longrightarrow \frac{3}{4} \leq \frac{a}{b} \leq \frac{7}{8}$

Out of the possible combinations of $a$ and $b$ , only $\frac{a}{b} = \frac{3}{4}$ satisfies this inequality.

If $5 \leq b \leq 8$ :

$\lfloor\frac{8}{b}\rfloor = 1 \Longrightarrow \lfloor\frac{8a}{b}\rfloor = 5$

$5 \leq \frac{8a}{b} \leq 6\Longrightarrow \frac{5}{8} \leq \frac{a}{b} \leq \frac{3}{4}$

Out of the possible combinations of $a$ and $b$ , $\frac{a}{b} = \frac{5}{7}$ and $\frac{a}{b} = \frac{5}{8}$ satisfies this inequality.

If $9 \leq b \leq 10$ :

$\lfloor\frac{8}{b}\rfloor = 0 \Longrightarrow \lfloor\frac{8a}{b}\rfloor = 4$

$4 \leq \frac{8a}{b} \leq 5\Longrightarrow \frac{1}{2} \leq \frac{a}{b} \leq \frac{5}{8}$

Out of the possible combinations of $a$ and $b$ , only $\frac{a}{b} = \frac{5}{9}$ satisfies this inequality.

Finally! We have our four solutions:

$\tan\theta_1=\frac{3}{4}$ , $\tan\theta_2=\frac{5}{7}$ , $\tan\theta_3=\frac{5}{8}$ , and $\tan\theta_4=\frac{5}{9}$

Therefore our answer must be $\boxed{4}$ .

First we have to realize that this chess board is the same as the first quadrant of a Cartesian plane. Let the inferior left corner be the origin of the plane and the board is the first quadrant. For this problem I wanted to create a function that spits out the number of squares of side length $l=1$ the line $f(x)=mx$ touches up to a certain $x_1$ . This function would be $g(m, x_1)$ which would obviously depend on the values of $m$ and $x_1$ . After giving it some thought and trying different ideas I arrived at the conclusion that:

$g(m,x_1)=\lceil mx_1\rceil, \hspace{0.2in} \mbox{if} \hspace{0.1in}m\in\mathbb{N}$ $g(m,x_1)=\lceil x_1\rceil + \lceil mx_1\rceil -1, \hspace{0.2in} \mbox{if} \hspace{0.1in}m\in\mathbb{P}$ $g(m,x_1)=\lceil x_1\rceil + \bigg\lfloor \frac{p}{q} x_1 \bigg\rfloor - \bigg\lfloor \frac{x_1}{q} \bigg\rfloor , \hspace{0.2in} \mbox{if} \hspace{0.1in}m\in\mathbb{Q}$

$\hspace{2.9in}$ Where $\lceil x \rceil$ is the ceil function and $\lfloor x \rfloor$ is the floor function .

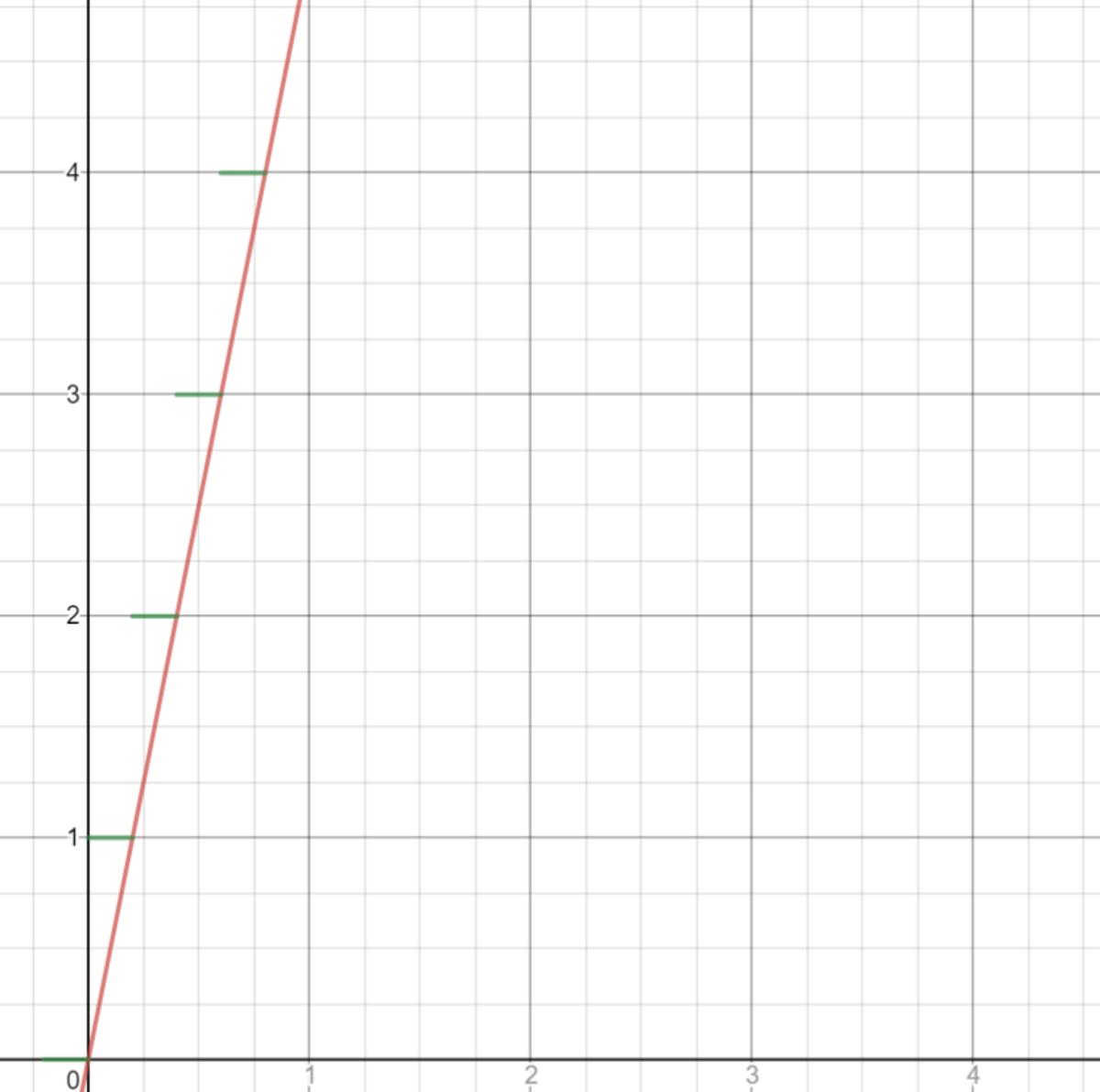
The function had to be split into three parts as all of these cases show different behaviors. If the slope is a natural number then the number of squares it touches up until $x_1$ is just $\lceil mx_1\rceil$ since $f(x)$ will touch a new square after its value surpasses a natural number, which is why we ceil the function. For example, the function $f(x)=5x$ touches one square in the range $0<x_1\leq \frac{1}{5}$ , or in other words, $0<f(x_1)\leq 1$ . The number of squares it touches only depends on the vertical part of the function, the $y$ value:

Now, with irrational numbers this does not happen. This is because if $m$ is an irrational number, the line will never touch the corner of a square ever again after leaving the origin. If $m$ was of the form $\frac{p}{q}$ the line would touch the corner of the square at the points of the form $(kq,kp)$ . But we can think of irrational numbers as the limit of a number of the form $\frac{p}{q}$ which has an infinitely big numerator and denominator, which is why they have infinite, and not finite, periods of decimals; namely $\pi=\dfrac{\displaystyle\lim_{p \to \infty_1} (p)}{\displaystyle\lim_{q \to \infty_2} (q)}$ .

The two numbers would grow in distinct ways, which leads to the particular ratio between them in the limit, which is the irrational number. This way of viewing them makes the fact that they don't touch the corner of a square again more evident, as it would technically require an infinitely big and special $x_1$ . Another way to view it is that you would need an irrational $x_1$ to obtain an integer in the y-axis, but that would give a point with an irrational $x_1$ and an integer in the y value, which is not the corner of a square. Similarly, if you plug an integer into the x value you will obtain an irrational in the y value, which is not the corner of a square.

Since it doesn't touch the corner of a square again when the values of the function are between 0 and 1 the number of squares it touches are simply the ceil of the x value: $0<f(x_1)\leq 1 \implies g(m,x_1)=\lceil x_1\rceil$ . For simplicity instead of thinking about the interval in which the values of the function fit (which is $0<f(x_1)\leq 1$ for the first level), I like to think about it as the ceil of $f(x)$ : $\lceil mx_1\rceil$ . So $\lceil mx_1\rceil=1 \implies g(m,x_1)=\lceil x_1\rceil$ . See the example $f(x)=\frac{\sqrt{2}}{2}x$ :

Observe that when $\lceil mx_1\rceil=1 \implies g(m,x_1)=\lceil x_1\rceil$

$\hspace{0.7in}$ When $\lceil mx_1\rceil=2 \implies g(m,x_1)=\lceil\frac{1}{m}\rceil+\lceil x_1\rceil-\lfloor\frac{1}{m}\rfloor$

$\hspace{0.7in}$ When $\lceil mx_1\rceil=3 \implies g(m,x_1)=\lceil\frac{1}{m}\rceil+\lceil\frac{2}{m}\rceil+\lceil x_1\rceil-\lfloor\frac{1}{m}\rfloor-\lfloor\frac{2}{m}\rfloor$

$\hspace{0.7in}\mbox{...}$

$\hspace{0.7in}$ When $\lceil mx_1\rceil=k \implies g(m,x_1)=\lceil x_1\rceil+\displaystyle\sum_{i=0}^{k-1}\bigg\lceil\frac{i}{m}\bigg\rceil-\bigg\lfloor\frac{i}{m}\bigg\rfloor$

Because $m$ is not an integer $\lceil\frac{i}{m}\rceil-\lfloor\frac{i}{m}\rfloor=1$ . So $\displaystyle\sum_{i=0}^{k-1}\bigg\lceil\frac{i}{m}\bigg\rceil-\bigg\lfloor\frac{i}{m}\bigg\rfloor=k-1$

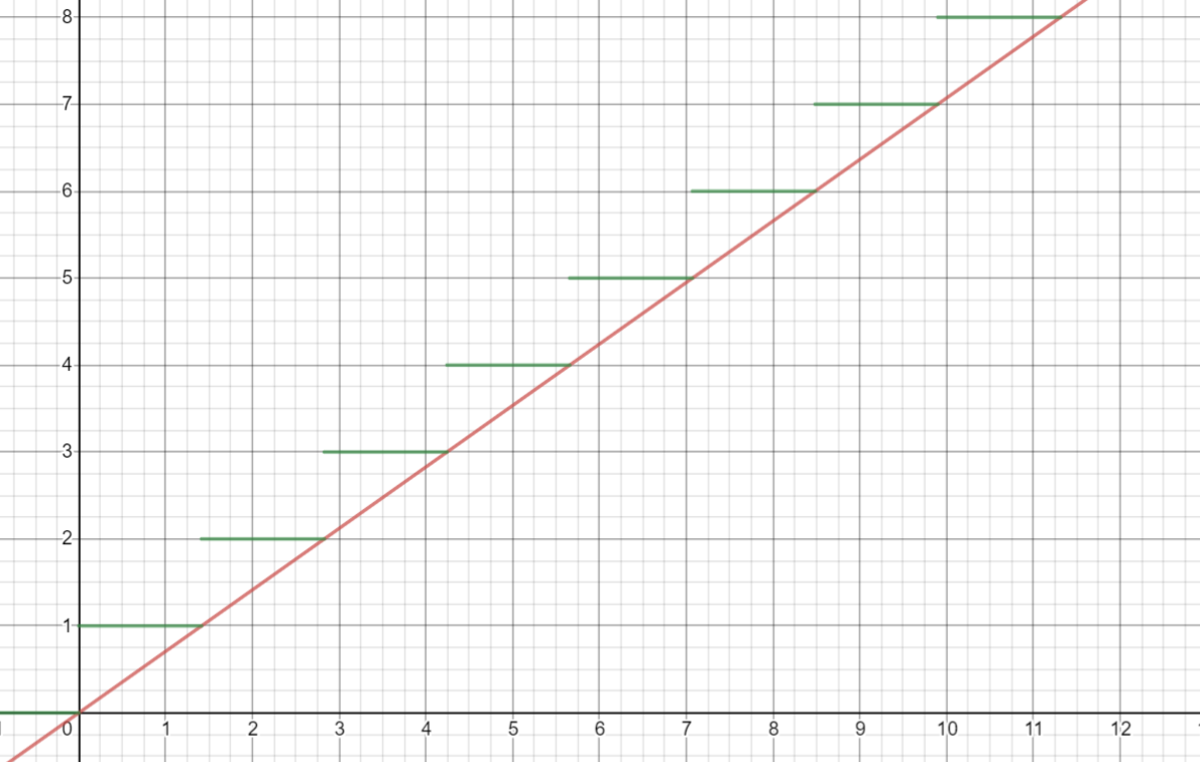
All in all: $g(m,x_1)=\lceil x_1\rceil+k-1=\lceil x_1\rceil+\lceil mx_1\rceil-1$ . This result can be interpreted the following way: when there is an irrational slope, apart from adding the squares touched by the vertical part of the line, which is the $\lceil x_1\rceil$ , you also add the vertical squares it touches; however it does it with a delay by one, since in the first level you don't have any extra vertical element, which explains the $\lceil mx_1\rceil -1$ .

Now with rational numbers something similar happens but with one key difference: a function with a rational slope $\frac{p}{q}$ will touch the corner of a square periodically, every multiple of $q$ in the x-axis. This implies that when it touches a corner it won't have the vertical increment the previous function for irrationals accounted for, so we need to find a way to remove it. Take a look at the case where $f(x)=\frac{3}{4}x$ touches a corner every multiple of 4, notice it isn't touching the square above to the left of the corner, which would otherwise be counted if we were talking about irrationals. It only touches another square diagonally after it passes through the corner:

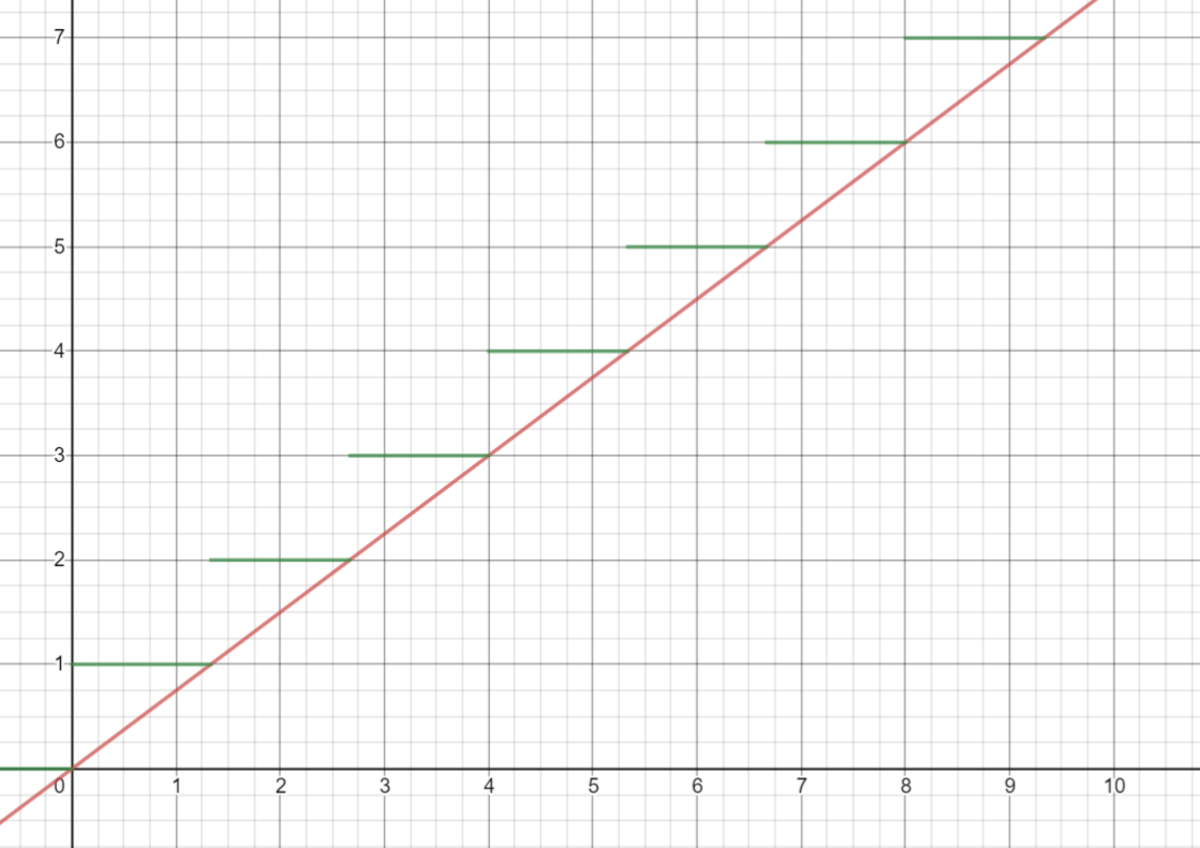
The term $\lfloor \frac{x_1}{q} \rfloor$ turns into a 1 in the moment $q\leq x_1< 2q$ , into a 2 when $2q\leq x_1 < 3q$ and so on. Subtracting this from the previous function will eliminate the traces of the vertical increment present in the previous function after passing through the multiples of $q$ in the x-axis. This results in: $g(m,x_1)=\lceil x_1\rceil+\lceil mx_1\rceil -1 -\lfloor \frac{x_1}{q} \rfloor$ .

Now, the problem is that when $x_1$ is a multiple of $q$ the -1 is subtracting an extra unit from the result, unit which the term $\lfloor \frac{x_1}{q} \rfloor$ already counts for. So at this moment that -1 should turn into a zero. We can do this by replacing the -1 with the term $-\lceil \{\frac{x_1}{q}\}\rceil$ . This term turns into a 0 when $x_1$ is a multiple of $q$ and to -1 otherwise. So we have: $g(m,x_1)=\lceil x_1\rceil+\lceil mx_1\rceil -\lceil \{\frac{x_1}{q}\}\rceil -\lfloor \frac{x_1}{q} \rfloor=\lceil x_1\rceil + \lfloor mx_1 \rfloor - \lfloor \frac{x_1}{q} \rfloor$ (As Garrett Clarke points out in the responses).

It is important to note that with the addition of the term $\lfloor \frac{x_1}{q} \rfloor$ , it is important to use coprime $p$ and $q$ numbers, or, put another way, simplified fractions. Avoid using decimals and use the whole coprime numbers that result from simplifying the fraction, as these are the ones that give the correct information. Another thing to note is that, technically, this function also works for natural numbers since it is the case with $q=1$ and $p\in\mathbb{N}$ where: $g(m,x_1)=\lceil x_1\rceil + \lfloor \frac{p}{1} x_1 \rfloor - \lfloor \frac{x_1}{1} \rfloor=g(m,x_1)=\lceil x_1\rceil + \lfloor px_1 \rfloor - \lfloor x_1 \rfloor$ . If $x_1$ has decimals then: $\lceil x_1\rceil + \lfloor px_1 \rfloor - \lfloor x_1 \rfloor=\lfloor px_1 \rfloor +1=\lceil px_1 \rceil$ . If it doesn't have decimals then: $\lceil x_1\rceil + \lfloor px_1 \rfloor - \lfloor x_1 \rfloor=x_1-x_1+\lfloor px_1 \rfloor=\lfloor px_1 \rfloor=\lceil px_1 \rceil$ . In both cases the only term that survives is $\lceil px_1 \rceil$ , which is exactly the function that we found previously for the case of the naturals. I presented these three cases to present the ideas behind each behavior depending the type of number of the slope as I originally conceived them, however it also makes a lot of sense to collect the naturals and the rationals into a single group that use the same function, after all, natural numbers are also rational. So now I'd rather write:

$g(m,x_1)=\lceil x_1\rceil + \lceil mx_1\rceil -1, \hspace{0.2in} \mbox{if} \hspace{0.1in}m\in\mathbb{P}$ $g(m,x_1)=\lceil x_1\rceil + \bigg\lfloor \frac{p}{q} x_1 \bigg\rfloor - \bigg\lfloor \frac{x_1}{q} \bigg\rfloor , \hspace{0.2in} \mbox{if} \hspace{0.1in}m\in\mathbb{Q}$

With all of this rationale behind, it is easy to find the cases in which Bobby touches exactly 12 squares in his chessboard when following a path that has a rational slope less than 1. The chess board has 8 squares of side length, so $x_1=8$ , the slope is of the form $m=\frac{a}{b}$ so we use the function for rational numbers. We also know the value of $g$ is 12. We plug in the values and simplify as follows:

$12=\lceil 8\rceil + \bigg\lfloor\frac{a}{b} \cdot8 \bigg\rfloor - \bigg\lfloor \frac{8}{b} \bigg\rfloor$ $4=\bigg\lfloor\frac{a}{b} \cdot8 \bigg\rfloor - \bigg\lfloor \frac{8}{b} \bigg\rfloor$

We can find that only 4 instances work:

$m=\frac{5}{8}\hspace{0.2in} m=\frac{3}{4}\hspace{0.2in} m=\frac{5}{7}\hspace{0.2in} m=\frac{5}{9}$

Since there's only 31 slopes to look at, it was easier to just plot all the paths and count up the ones that crossed exactly 12 squares. Was that a cheat? Or just a Neanderthal bash?

Counting up the crossings is made easier if one keeps in mind that if the denominator is less than $9$ , then the line crosses at the corner somewhere, and sometimes more than once. In fact, one can use this to help plot the lines.