Walking At Random (Logic)

Logic Level 2

Imagine that you are walking along the lines of the grid of unit squares below.

If you start from the bottom left-hand corner and walk along the lines until you return to your starting point, what is the length of the longest path you can make if you can't travel on the same line segment or pass through the same point twice?

The answer is 24.

4 solutions

Brian Galebach
Aug 6, 2015

Proving that the answer is at least 24 is simple. Draw one of the many paths that returns to the original point in 24 steps. However, the question asks to find the longest path. Therefore we must prove that 25 is impossible. Consider that after n steps, the sum of the coordinates of the location (x,y) mod 2 will always be n mod 2, because we either change x or y by one in each step. After 25 steps, (x,y) cannot be (0,0), our starting location. So a path length of 25 is impossible, thus confirming 24 as the answer.

Beautiful solution, I love it!

Garrett Clarke - 5 years, 10 months ago

Buy if you can't pass through the same point twice, how can your finish point be your start? (semantics)

Daniel Richards - 5 years, 6 months ago

I think that’s the only exception

anjaly jeyacanthan - 1 year, 1 month ago

that is a really good solution. I just have a question though, how can you prove that the answer can't be 26? I am assuming it is something to do with the fact that there are only 25 dots.

Aviral Jain - 5 years, 10 months ago

The answer can't be 26 due to the construction of the problem. You can't return to a point you've already been to, so no matter what we have an upper bound of at most 25 because there are only 25 points on the grid.

Garrett Clarke - 5 years, 10 months ago

DEAR AUTHOR!! you can put into the initial text of the puzzle an illustrative picture of any line which could be obtained by following the puzzle's rules for, let's say, 4 squares grid! that would help a lot!!!!!

Nik Gibson - 2 years, 9 months ago

Jaques Jonas
Aug 6, 2015

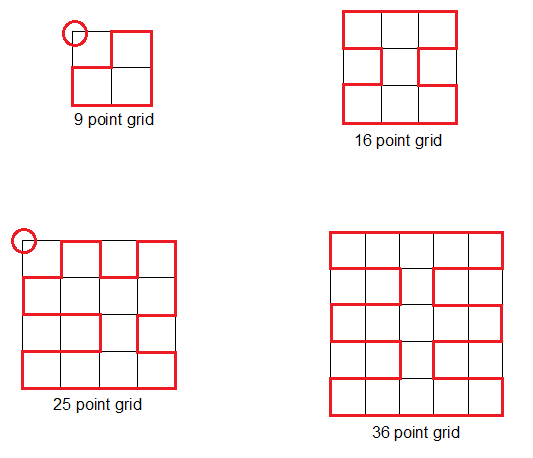
In a n point grid, if n is an odd number, it's only possible to reach n-1 points in the grid without passing the same point twice. The picture below shows it clearly. This is caused by the assimetry in the grids with an odd number of points.

Garrett Clarke
Aug 1, 2015

Here is an example of the solution:

This answer is by no means unique, in fact there are 411 other ways to achieve the maximum length of 24.

Yea, did same. :D

Sidhartha Khare - 5 years, 10 months ago

Dear Garrett, how did you calculate the 412 ways to achieve length of 24 ?

Satyen Nabar - 4 years, 10 months ago

Bump .. would like to know how the 412 answer was achieved also

Mark Wishart - 11 months, 3 weeks ago

Michael Mendrin
Aug 1, 2015

There are 25 points, so that if each point is visited just once, then there's 2 x 25 = 50 segments traveled, divided by 2 because they're counted twice. Hence, 25 segments is the maximum possible path. Hoo hah. That's logic. Even though 24 is the correct answer.

Love me some logic! If the grid size was an odd number then we could reach every point, but for even sized grids you'll have to let one point go every time. In other words, the maximum path you can make depends on the parity of the board size.

Garrett Clarke - 5 years, 10 months ago

We can pass through each point only once , so if a point is connected to three or four lines,only two of them would be used, thus if a point is connected to 3 lines, one would be left out, two if it is connected to four, so by counting the number of the lines that we wouldn't use, we obtain 16 lines, the total number of lines is 40, so 40-16=24 Then the answer is 24

Mahaba Al Sahili - 1 year, 8 months ago

Walking At Random (Logic)

The answer is 24.

4 solutions

0 pending reports