Walking carefully on a grid - 1

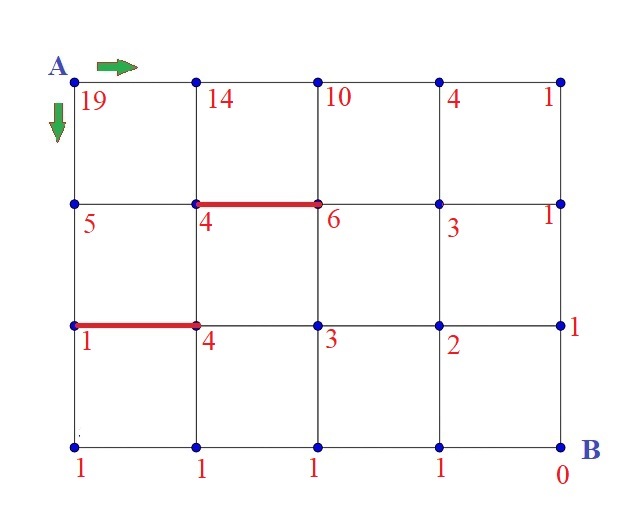
You need to make a total of 7 moves, and 3 must be down while 4 must be right. Therefore, there are ${7 \choose 3}=35$ ways to choose the 3 moves to go down if there are no red lines.

We can subtract the amount of paths that go through a red line.

If we pass through the bottom left red line, there is one way to get to the red line, and 4 ways to get to the bottom right corner afterwards.

If we pass through the top right red line, there are 2 ways to get to the red line, and ${4 \choose 2 }=6$ ways to get to the bottom right corner afterwards, so in total, there are $2 \times 6 =12$ ways.

$35-4-12=\boxed{19}$

Easy approach: