Walking in a Rectangular Grid Warmup
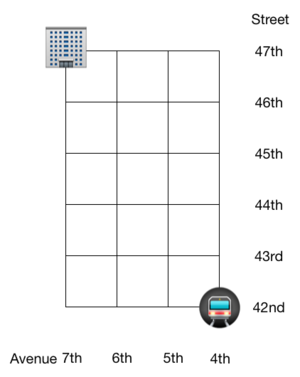 As a tourist in NY, I want to go from the Grand Central Station
street and
avenue
to Times Square
street and
avenue
As a tourist in NY, I want to go from the Grand Central Station
street and
avenue
to Times Square
street and
avenue
If I only walk West and North, how many ways are there for me to get there?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution 1: We will be walking 8 blocks, of which 3 are west and 5 are north. Thus, the number of ways is ( 3 8 ) = 5 6 .
Solution 2: Starting from the lower right, we label the number of ways to get to a particular intersection by just going north or west. This can be obtained by finding the sum of the number of ways from an intersection that is south or east of it.
Hence, the answer is 56.