You Can Only Walk This Way!
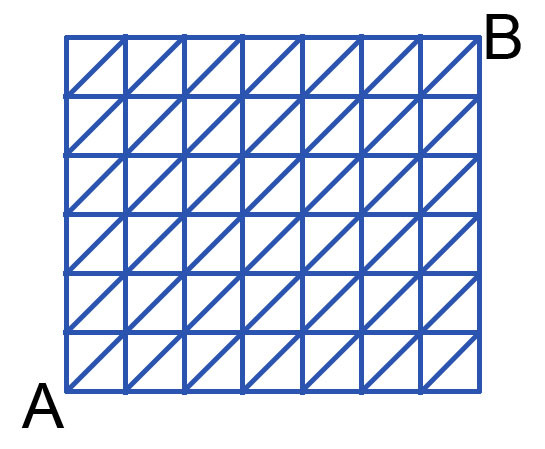
Mr. Truong is stationed at point A and needs to make it to point B to give a lecture there. However, to make sure he can reach there on time, he decides only to go by 3 directions: up, right or up-right. In how many different routes can he go?
The answer is 19825.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I did something similar, I analyzed the different cases in which we take 1,2,...,6 diagonal moves. For examples, if we take 3 diagonal moves, then we are left to make 4 right and 3 up moves. 7C3 times the number of ways to make the diagonal moves, which is "combination with replacement" and has formula nHr = (n+r-1)C r , since we are "putting" the 3 diagonal moves anywhere between the up/right moves. So we are calculating 8H3 =10C3 in this case. Summing up all 7 cases gives the same answer.
Even I did it the same way,but how did you evaluate the final summation ?
Let Mr.Truong travel d diagonals. The remaining 1 3 − 2 d sides,he travels up or right, which can be done in ( 7 − d 1 3 − 2 d ) ways. The d diagonals can be placed in ( d 1 3 − d ) ways.
So the total number of ways= d = 0 ∑ 6 ( 7 − d 1 3 − 2 d ) ( d 1 3 − d ) .
This summation turns out as 1 9 8 2 5
Let a n , m be the number of different routes for a grid of n × m
We are looking for a 7 , 6
We can easily see that : a n , m = a n − 1 , m + a n , m − 1 + a n − 1 , m − 1 for n, m positive integers a n , 0 = a 0 , n = 1 for n integer
With spreadsheet, we can have the result 19825
Nice, answer @Abdelhamid Saadi ! This is the way I did it as well... ;)
If Mr. Truong just goes up and right, he must walk up 6 times and walk right 7 . So, in total, he must walk 1 3 little lines of the grid. Every diagonal he walks is a shortcut: indeed, he walks up and right every time he walks up-right. This means that for each up-right line he walks, he's walking a line less than if he walks up and then right.
As the grid has 6 diagonals, we can reinterpret the problem as follows:
We have 6 letters U , 7 R ′ s and 6 D ′ s . In how many ways can we organize the U ′ s and R ′ s ? 7 ! ⋅ 6 ! 1 3 ! ; every time we write one D in each setup we have created previously, we erase one U and one R from each one.
Thus, when we write 1 D , we have 6 R ′ s and 5 D ′ s . The number of ways in which we can organize this letters is 6 ! ⋅ 5 ! 1 2 ! .
We can continue writing and removig letters until we have 6 D ′ s and just 1 R .
At the final, we will have the following sum:
∑ k = 0 6 ( 7 − k ) ! ⋅ ( 6 − k ) ! ⋅ k ! ( 1 3 − k ) ! , in which k is the number of D ′ s in the setup.
Therefore, when we calculate that sum, the total different routes in which Mr. Truong can go from A to B are 1 9 8 2 5 .