Walking on a grid
George and John walk along the lines of a grid with George (labelled 'G') starting from the bottom-left corner and John (labelled 'J') starting from the top-right corner. George can only walk to the top or to the right while John can only walk to the bottom or to the left.
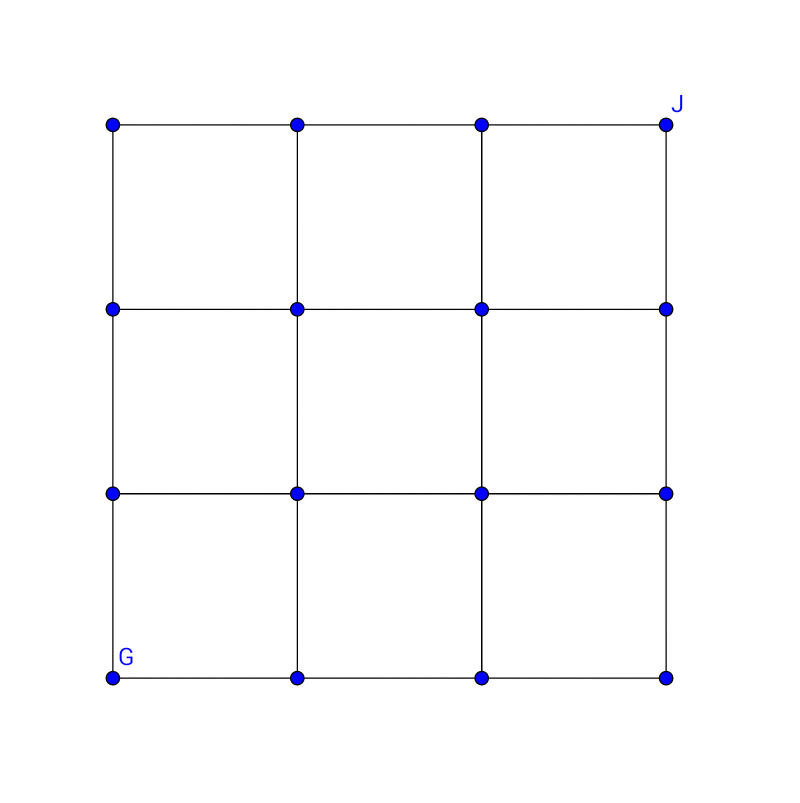
Find the total number of ways in which they can meet at the lattice points shown in the grid.
Clarification :-
- The speeds of George and John are not necessarily equal.
- It is possible for George not to move at all and John to travel along a route from the entire grid so that they meet at G. Conversely, they can also meet at J, if John doesn't move and George travel a route from the grid shown.
This problem is original.
The answer is 140.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Lets take the grid into co-ordinate plane as shown below.
The diagnol shown is y = x . Observe that the number of points required for reaching at lattice points which are images with respect to each other through this line have the same value. So, we would find the number of ways of reaching the points for which y > x only and then double them in the final answer for the points satisfying y < x . The points lying on y = x need to be counted only once.
The formula which is going to be used throughout this question is:- The number of ways of crossing a m × n grid = m ! × n ! ( m + n ) !
For point A, George can travel only through the straight line AG. John also can only travel through JA. So, the number of ways is 1 .
For point B, George can travel only along BG, while John can swap region ABPJ. The number of ways of crossing this is 3 ! 4 ! . So, number of ways = 1 × 3 ! 4 ! = 4 .
For point C, George can travel only along CG, while John can swap region ACOJ. The number of ways of crossing this is 3 ! × 2 ! 5 ! . So, number of ways = 1 × 3 ! × 2 ! 5 ! = 1 0 .
For point D, George can swap region ADKG i.e. 3 ! 4 ! ways, while John can only travel along DJ. So, number of ways = 3 ! 4 ! × 1 = 4 .
For, point E, George can swap region BGKE i.e 2 ! 3 ! ways while John can swap region DEPJ i.e, 2 ! 3 ! ways. So, number of ways = 2 ! 3 ! × 2 ! 3 ! = 9 .
For point F, George can swap region AFLG i.e. 3 ! × 2 ! 5 ! ways, while John can only travel along FJ. So, number of ways = 3 ! × 2 ! 5 ! × 1 = 1 0 .
So, for points y > x , total ways = 1 + 4 + 1 0 + 9 + 1 0 = 3 8 .
Therefore, for points y < x , total ways = 3 8 .
For, point G, George needn't move while John can swap region AGNJ i.e, 3 ! × 3 ! 6 ! ways. So, number of ways = 1 × 3 ! × 3 ! 6 ! = 2 0 .
For, point H, George can swap region CGKH i.e 1 ! × 1 ! 2 ! ways while John can swap region DEPJ i.e, 2 ! × 2 ! 4 ! ways. So, number of ways = 2 ! × 2 ! × 2 ! 4 ! = 1 2 .
For, point I, number of ways is similar to that of H (by symmetry) = 1 2 .
For, point J, number of ways is similar to that of G (by symmetry) = 2 0 .
So, for points y = x , total ways are 2 0 + 1 2 + 1 2 + 2 0 = 6 4 .
So, the net number of ways = 3 8 + 3 8 + 6 4 = 1 4 0 .